Kezdőlap


Feladat:	2003. évi Nemzetközi Matematika Diákolimpia 11. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Paulin Roland
Füzet:	2004/október, 386 - 387. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Háromszög nevezetes körei, Thalesz tétel és megfordítása, Húrnégyszögek, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 2004/szeptember: 2003. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Paulin Roland megoldása. Thálész tétele alapján $B M C ∢ = B N C ∢ = 90^{\circ}$ , így $M$ és $N$ a magasságok talppontjai, melyek az $A B C$ háromszög $A B$ , illetve $A C$ oldalainak belsejében vannak, mert a háromszög hegyesszögű.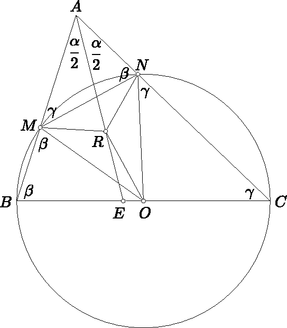
$B M N C$ húrnégyszög, így $A M N ∢ = γ$ , $A N M ∢ = β$ . $O B M$ és $O C N$ egyenlő szárú háromszögekben $O M B ∢ = β$ , $O N C ∢ = γ$ , vagyis $O M N ∢ = O N M ∢ = α$ , $M O N ∢ = π - 2 α$ .

Belátjuk, hogy a

B A C

és

M O N

szögek szögfelezői ‐

e

és

f

‐ nem párhuzamosak, így

R

egyértelműen meghatározott.

e ∥ f

esetén legyen

f \cap A C = D

. A

D O C

háromszögben

D

-nél

\frac{α}{2}

C

-nél

γ

O

-nál

\begin{matrix} C O N ∢ + \frac{N O M ∢}{2} = \\ = (π - 2 γ) + \frac{π - 2 α}{2} = \frac{3}{2} π - 2 γ - α \end{matrix}

szög van, így a szögösszeg

\begin{matrix} π = \frac{α}{2} + γ + \frac{3}{2} π - 2 γ - α . \end{matrix}

Rendezve:

\begin{matrix} \frac{α}{2} + γ = \frac{π}{2} \Rightarrow α + 2 γ = π = α + β + γ \Rightarrow γ = β \Rightarrow A B = A C . \end{matrix}

Ezt a feltétel kizárja, így

e ∦ f

.
Legyen

I

O M N

háromszög beírt körének középpontja.

I M N ∢ = I N M ∢ = \frac{α}{2}

miatt

M I N ∢ = π - α

, ezért

A M I N

húrnégyszög, így

I A N ∢ = I M N ∢ = \frac{α}{2}

. Tehát

I \in e

, ugyanakkor

I \in f

is teljesül, ezért

R = I

.
Legyen

E = e \cap B C

. Ez a

B C

oldal egy belső pontja. Belátjuk, hogy a

B M R

és a

C N R

háromszögek körülírt köre is átmegy

E

-n.

R E B ∢ = A E B ∢ = π - β - \frac{α}{2}

R E C ∢ = A E C ∢ = π - γ - \frac{α}{2}

, míg

R M B ∢ = β + \frac{α}{2}

R N C ∢ = γ + \frac{α}{2}

, így

R M B ∢ + R E B ∢ = R N C ∢ + R E C ∢ = π

. Azaz

R M B E

és

R N C E

húrnégyszögek, így az

R M B

és az

R N C

háromszögek körülírt körének van közös pontja a

B C

oldalon.