Kezdőlap


Feladat:	3670. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kiss Péter , Szabó Áron
Füzet:	2004/május, 310 - 312. oldal		PDF \| MathML
Témakör(ök):	Gördülés vízszintes felületen, Ütközés fallal, Feladat
Hivatkozás(ok):	Feladatok: 2003/december: 3670. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Mivel a fal tökéletesen sima, ütközéskor a labdára nem hat forgatónyomaték, tehát a szögsebessége az ütközés során változatlan marad. A labda tömegközéppontjának sebessége az ütközéskor ellentétes irányú lesz, nagysága pedig az eredeti sebesség $k$ -szorosa ( $k < 1$ az ütközési szám).
A falról visszapattanó labda ,,köszörülni'' kezd, majd az asztallap által kifejtett súrlódási erő előbb-utóbb csúszásmentes gördülésre kényszeríti. A mozgás részletes leírásához szükségünk lesz a labda tehetetlenségi nyomatékára. Mivel a pingponglabda vékony gömbhéj, tehetetlenségi nyomatéka két majdnem egyforma sugarú gömb tehetetlenségi nyomatékának különbségeként adható meg:

\begin{matrix} Θ = \frac{2}{5} m_{1} \cdot {(r + Δ r)}^{2} - \frac{2}{5} m_{2} \cdot r^{2}, \end{matrix}

ahol

\begin{matrix} m_{1} = \frac{4 π}{3} ϱ \cdot {(r + Δ r)}^{3}, illetve m_{2} = \frac{4 π}{3} ϱ \cdot r^{3}, \end{matrix}

a gömbhéj tömege és a sűrűsége közötti kapcsolat pedig

\begin{matrix} m = \frac{4 π}{3} ϱ \cdot {(r + Δ r)}^{3} - \frac{4 π}{3} ϱ \cdot r^{3} . \end{matrix}

Ezekből a képletekből

Δ r ≪ r

esetén

\begin{matrix} Θ = \frac{2}{5} m \frac{{(r + Δ r)}^{5} - r^{5}}{{(r + Δ r)}^{3} - r^{3}} \approx \frac{2}{3} m r^{2} \end{matrix}

adódik.
Az ábra egy

v_{0}

sebességgel,

ω_{0}

szögsebességgel (

v_{0} = r ω_{0}

) a falnak ütköző labdát ábrázol közvetlenül az ütközés után.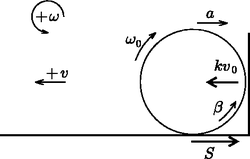

Az ábrán bejelölt

v

és

ω

irányokat tekintve pozitívnak, a mozgásegyenletek:

\begin{matrix} S = m a, S r = Θ β, \end{matrix}

ezekből a gyorsulás és a szöggyorsulás

\begin{matrix} a = \frac{S}{m}, β = \frac{S r}{Θ} = \frac{3}{2} \cdot \frac{S}{m r}, \end{matrix}

tehát

t

idő múlva a labda sebességének és szögsebességének előjeles nagysága:

\begin{matrix} v = k v_{0} - a t, ω = β t - ω_{0} . \end{matrix}

A csúszásmentes gördülés akkor kezdődik, amikor

v = r ω

vagyis

\begin{matrix} k v_{0} - \frac{S}{m} t = (\frac{S r}{Θ} t - ω_{0}) r \end{matrix}

fennáll, tehát

\begin{matrix} t = \frac{k v_{0} + r ω_{0}}{1 + \frac{m r^{2}}{Θ}} \cdot \frac{m}{S} = \frac{2}{5} \cdot \frac{m}{S} v_{0} (k + 1) \end{matrix}

idő múlva, s ekkor a labda sebessége

\begin{matrix} v = v_{1} = \frac{3 k - 2}{5} v_{0} . \end{matrix}

Látható, hogy ha

k \geq \frac{2}{3}

, akkor

v_{1} \geq 0

, vagyis a köszörülés befejeztekor a labda balra mozog (vagy éppen megáll), ilyenkor nem ütközhet ismét a fallal.
Második ütközés csak akkor következik be, ha

k < \frac{2}{3}

, tekintsük tehát ezt az esetet. Amennyiben a labda csúszásmentesen gördülve ér vissza a falhoz

\begin{matrix} | v_{1} | = \frac{2 - 3 k}{5} v_{0} \end{matrix}

sebességgel, akkor ugyanaz történik, mint az első ütközés után, csak

v_{1}

játssza

v_{0}

szerepét, azaz köszörülés, majd tiszta gördülés után a labda

\begin{matrix} | v_{2} | = \frac{2 - 3 k}{5} | v_{1} | = {(\frac{2 - 3 k}{5})}^{2} v_{0} \end{matrix}

sebességgel harmadszor is nekiütközik a falnak, és így tovább (elvben) a végtelenségig. Pontosan 2 ütközés tehát ebben az esetben sem valósulhat meg.
Előfordulhat-e az, hogy a labda hamarabb ér vissza a falhoz, mintsem a tiszta gördülés feltétele teljesülhetne? Ennek feltétele az, hogy a

k v_{0}

kezdősebességgel és

a

gyorsulással mozgó labdának a falhoz visszaérkezéséig eltelő

t_{0}

idő kisebb legyen, mint a köszörülés megszűnéshez szükséges, korábban kiszámított

t

idő:

\begin{matrix} t_{0} = 2 \frac{k v_{0}}{a} < \frac{2}{5} \cdot \frac{m}{S} \cdot v_{0} (k + 1) = \frac{2}{5} \cdot \frac{v_{0}}{a} (k + 1) = t, \end{matrix}

ami

k < \frac{1}{4}

esetén áll fenn.
Vizsgáljuk a továbbiakban ezt az esetet! A labda az első és a második ütközés között ugyanannyi ideig lassult, mint gyorsult, tehát a sebességének nagysága a második ütközés előtt ugyanakkora, mint az első ütközés után, nevezetesen

k v_{0}

, a második ütközést követően tehát a labda

k^{2} v_{0}

sebességgel pattan el a faltól. A szögsebesség közvetlenül a második ütközés előtt (és ami ezzel egyező, közvetlenül utána is) a forgómozgás egyenletéből kapható meg:

\begin{matrix} ω_{1} = - ω_{0} + β t_{0} = - ω_{0} + \frac{3}{2} \cdot \frac{S}{m r} \cdot 2 \frac{k v_{0}}{a} = (3 k - 1) ω_{0} . \end{matrix}

A második ütközés után a köszörülés addig tart, míg fenn nem áll

\begin{matrix} k^{2} v_{0} - a t = ω_{1} + r β t = (3 k - 1) r ω_{0} + \frac{3}{2} \cdot \frac{a}{r} \cdot r t, \\ t = t' = \frac{2}{5} \cdot \frac{v_{0}}{a} (k^{2} - 3 k + 1) & (*) \end{matrix}

idő múlva következik be. Ennyi idő alatt a labda sebessége

\begin{matrix} v' = v_{1} - a t' = k^{2} v_{0} - \frac{2}{5} (k^{2} - 3 k + 1) v_{0} = \frac{1}{5} (3 k^{2} + 6 k - 2) v_{0} \end{matrix}

lesz. Ha ez a sebesség pozitív lenne, akkor harmadik ütközés nem jöhetne létre. A

3 k^{2} + 6 k - 2

kifejezés azonban csak

\begin{matrix} k > \sqrt[]{\frac{5}{3}} - 1 \approx 0, 29 > \frac{1}{4}, \end{matrix}

illetve

k < - 2, 29

tartományban lenne pozitív. Számunkra mindkét lehetőség elfogadhatatlan, az első azért, mert ellentmond a köszörülve ütközés

k < \frac{1}{4}

feltételének, a másik tartomány pedig fizikailag értelmetlen.
Összefoglalva megállapíthatjuk, hogy

k \geq \frac{2}{3}

esetén pontosan 1 ütközés zajlik le,

\frac{2}{3} > k \geq \frac{1}{4}

esetén tetszőlegesen sok ütközés, és ha

k < \frac{1}{4}

, akkor is legalább 3-szor ütközik a labda a falnak. Pontosan kettő ütközés tehát nem jöhet létre!