Kezdőlap


Feladat:	3595. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bóka Gergely , Paulin Dániel , Vigh Máté
Füzet:	2004/február, 110 - 112. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Tömegközéppont megmaradása, Feladat
Hivatkozás(ok):	Feladatok: 2003/február: 3595. fizika feladat

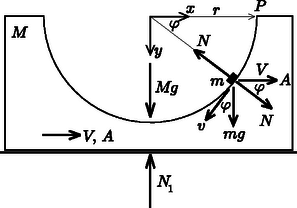
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a mélyedés sugarát $r$ -rel, a kérdéses nyomóerő nagyságát pedig (a $φ$ szögű helyzetben) $N$ -nel! A kis testre az $m g$ gravitációs erő és a hasáb nyomóereje hat. A hasábra a kis testre kifejtett nyomóerő ellenereje, az $M g$ gravitációs erő és az asztal által kifejtett $N_{1}$ nyomóerő hat.

A hasábra ható erők függőleges komponensei kiegyenlítik egymást, hiszen a hasáb függőleges irányban nem gyorsul. A hasáb vízszintes irányú

A

gyorsulását a vízszintes erők eredője (jelen esetben a kis test nyomóerejének vízszintes komponense) határozza meg:

\begin{matrix} A = \frac{N cos φ}{M} . \end{matrix}

(1)

A kis test a hasábhoz képest körmozgást végez. Jelöljük a kis testnek a hasábhoz viszonyított (relatív) sebességét (a kérdéses helyzetben)

v

-vel! Ezen sebesség segítségével ki tudjuk számítani a kis test hasábhoz viszonyított gyorsulásának sugár irányú komponensét:

\begin{matrix} a_{r} = \frac{v^{2}}{r} . \end{matrix}

(2)

Írjuk fel a kis test Newton-féle mozgástörvényének sugár irányú komponensét az asztalhoz rögzített (nem gyorsuló) koordináta-rendszerben:

\begin{matrix} N - m g sin φ = m (a_{r} - A cos φ) . \end{matrix}

(3)

Az (1) és (2) egyenletekből meg tudnánk határozni a keresett

N

erőt, ha

a_{r}

-t ismernénk, ehhez viszont (2) alapján a

v

ismeretére lenne szükségünk. A relatív sebesség meghatározására az energiamegmaradás törvénye nyújt lehetőséget.
A kis testnek az asztalhoz viszonyított sebességét a

\begin{matrix} v_{y} = v cos φ \end{matrix}

(4)

függőleges és a

\begin{matrix} v_{x} = V - v sin φ \end{matrix}

(5)

vízszintes komponensekkel jellemezhetjük, ahol

V

a hasáb sebessége az asztalhoz képest. Az impulzusmegmaradás törvénye szerint a rendszer kezdeti (nulla) impulzusának vízszintes komponense a mozgás során nem változik:

\begin{matrix} m v_{x} + M V = 0. \end{matrix}

(6)

Végül az energiamegmaradás törvénye:

\begin{matrix} \frac{1}{2} m (v_{x}^{2} + v_{y}^{2}) + \frac{1}{2} M V^{2} = m g r sin φ . \end{matrix}

(7)

A (4)‐(7) egyenletekből kiszámíthatjuk a kis test és a hasáb relatív sebességét:

\begin{matrix} v = \sqrt[]{\frac{2 (M + m) g r sin φ}{M + m cos^{2} φ}}, \end{matrix}

majd ebből az (1)‐(3) egyenletek segítségével adódik a keresett nyomóerő:

\begin{matrix} N (φ) = \frac{3 M + 2 m + m cos^{2} φ}{{(M + m cos^{2} φ)}^{2}} M m g sin φ . \end{matrix}

(8)

Ez az erő kezdetben (a

P

pontnál) nulla,

φ

növekedtével egyre nő, és

φ = 90^{\circ}

-nál éri el a maximumát:

N_{{max}_{}^{}} = (3 + \frac{2 m}{M}) m g

. Ha

M ≫ m

(rögzítettnek tekinthető hasáb esete), akkor a kis test a pálya legalsó pontjában a nyugvó helyzetben mérhető súlyának 3-szorosával nyomja a hasábot. A másik határeset:

M ≪ m

, ekkor a kis test csaknem szabadon esik, a nyomóerő majdnem mindig elhanyagolhatóan kicsi, csupán az alsó fordulópontban válik egy rövid időre nagyon naggyá.

II. megoldás. Jelöljük (az I. megoldás ábráján bejelölt koordináta-rendszer irányítását használva) a hasáb elmozdulását

X

-szel, a kis test koordinátáit pedig

x

-szel és

y

-nal! A rendszer tömegközéppontjának vízszintes koordinátája ‐ vízszintes külső erő hiányában ‐ nem változhat meg:

\begin{matrix} \frac{m x + M X}{m + M} = \frac{m r}{m + M} . \end{matrix}

(9)

Másrészt a kis test a mélyedés középpontjától mindvégig

r

távolságra kell legyen:

\begin{matrix} {(x - X)}^{2} + y^{2} = r^{2}, \end{matrix}

(10)

ahonnan (9) felhasználásával

\begin{matrix} \frac{{(x - x_{0})}^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{matrix}

(11)

adódik, ahol

a = \frac{M}{M + m} r

b = r

és

x_{0} = \frac{m}{M + m} r

. (11) egy olyan ellipszis egyenlete, amelynek féltengelyei

a

és

b

hosszúak, és a középpontja az

(x_{0}; 0)

koordinátájú pont.
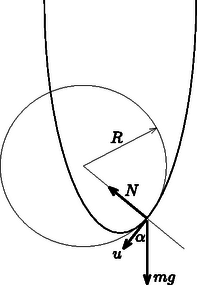
Az energiamegmaradás törvényének felhasználásával a pálya bármely pontjában meg tudjuk adni a kis test (inerciarendszerbeli) sebességének nagyságát (jelöljük ezt

u

-val), és a sebesség irányát is (legyen a sebességvektor függőlegessel bezárt szöge

α

A mozgásegyenletnek a pillanatnyi sebességre merőleges komponense szerint

\begin{matrix} N - m g sin α = m \frac{u^{2}}{R}, \end{matrix}

(12)

ahol

R

az ellipszis megfelelő pontjához tartozó görbületi sugara. Ez utóbbi a matematikai kézikönyvekben megtalálható képletekkel kiszámítható, de elemi eszközökkel, pl. a bolygómozgás vagy a rezgőmozgás fizikai törvényeiből is meghatározható:

\begin{matrix} R = a^{2} b^{2} {[\frac{{(x - x_{0})}^{2}}{b^{4}} + \frac{y^{2}}{b^{4}}]}^{3 / 2} . \end{matrix}

Innen (12) alapján (

u

kiszámítható értékének felhasználásával) a nyomóerő nagyságának

φ

-vel kifejezett értékére az I. megoldásban megkapott (8) képlet adódik.