Feladat: B.3630 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bartha Emőke 
Füzet: 2004/március, 151 - 152. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai szerkesztések, Kör geometriája, Érintőnégyszögek, Feladat
Hivatkozás(ok):Feladatok: 2003/március: B.3630

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A körvonalon adott három pont három, közös belső pont nélküli körívre osztja a körvonalat. Ezen körívek belső pontjai jöhetnek számításba a keresett érintőnégyszög negyedik csúcsaként. Meg fogjuk mutatni, hogy mindegyik köríven pontosan egy alkalmas pont található.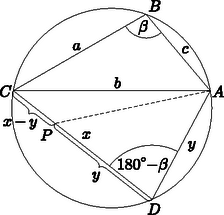

 
 

Válasszuk ki az egyik körívet tetszőlegesen, a körív két végpontját jelölje A és C, a harmadik adott pontot pedig B. A kiszemelt köríven keressük a négyszög negyedik csúcsát, a D pontot.
Az AD=y, CD=x jelöléssel teljesül, hogy a+y=c+x, azaz a-c=x-y, hiszen egy konvex négyszög pontosan akkor érintőnégyszög, ha szemközti oldalainak összege egyenlő.
Ha a>c, akkor x>y. (Az ábrán ez az eset látható.) A CD szakasz P pontja legyen olyan, hogy arra PD=AD=y teljesüljön, így PC=x-y=a-c. Mivel az ABCD négyszög húrnégyszög, azért PDA∢=180∘-β, az APD háromszög pedig egyenlő szárú, így PAD∢=APD∢=β2. Ezért APC∢=180∘-β2. A P pontból így az AC szakasz 180∘-β2 szögben látszik, tehát P rajta van az AC szakasz megfelelő, 180∘-β2 szögű látószögkörívén.
Ugyanakkor CP=a-c, így P az előbb említett látókörívnek és a C középpontú a-c sugarú körnek a közös pontja.
Ez a metszéspont mindig létrejön és egyértelműen meghatározott, mert a látókörív (180∘-β2>180∘-β miatt) a körülírt körön belül van; a-c pedig kisebb b-nél az ABC háromszögre felírható háromszög-egyenlőtlenség szerint. A P pont tehát szerkeszthető, és segítségével nyilván a D pont is: a C kezdőpontú CP félegyenes és az eredeti kör metszéspontja.
Szerkesztésünk nyilvánvalóan helyes, hiszen a fenti lépések után valóban azt kapjuk az ABCD húrnégyszögre (ami konvex), hogy c+CD=a+AD, azaz az ABCD négyszög érintőnégyszög is egyben.
Ha a=c, akkor az ABC töröttvonal bármely ,,beleírható'' körrel együtt tengelyesen szimmetrikus az AC szakasz felező merőlegesére. Így a C pontból és az A pontból egy ilyen körhöz húzott másik érintők is egymás tükörképei erre az egyenesre nézve, vagyis éppen e felezőmerőlegesen metszik egymást. Akkor lesz az ABCD négyszög érintőnégyszög, ha van olyan kör, amelyet a négyszög minden oldala érint. Az eddigiekből következik, hogy ebben az esetben a D pont csak az AC szakasz felező merőlegesén lehet, ez az egyenes metszi ki tehát az eredeti körből D-t. Ekkor deltoidot kapunk.
(Az a<c esetet nem kell tárgyalnunk, hiszen ha nem egyenlő ez a két szakasz, választhatjuk a nagyobbat a-nak a betűzéskor.)
Egyik esetben sem használtuk fel a β szög nagyságát. Szerkesztésünk mindkét esetben tetszőleges nagyságú β szög esetén elvégezhető, tehát akármelyik ívet kiválaszthatjuk a szerkesztés kezdetén. A szerkesztésből kiderül, hogy 1-1 köríven pontosan 1 jó D pont lesz, tehát bármely megadott ponthármashoz három megoldás tartozik.