Kezdőlap


Feladat:	3421. fizika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	2001/november, 502 - 504. oldal		PDF \| MathML
Témakör(ök):	Egyenesvonalú mozgás, Feladat
Hivatkozás(ok):	Feladatok: 2001/március: 3421. fizika feladat

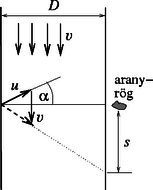
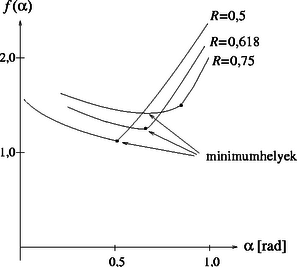
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a folyó szélessége $D$ , a víz sebessége $v$ , és jelölje $u$ azt a sebességet, amivel Joe futni, illetve evezni tud. Tegyük fel, hogy Joe először átevez a folyón, majd a partot érés helyétől a part mentén gyalog megy az aranyröghöz. (Természetesen az evezés és a gyaloglás sorrendje felcserélhető.) Ha csónakja vízhez viszonyított sebessége a vízével $π / 2 + α$ szöget zár be, a folyóra merőlegesen $u cos α$ sebességgel halad, miközben $v - u sin α$ sebességgel csurog lefelé (1. ábra). Ennek megfelelően

\begin{matrix} t_{1} = \frac{D}{u cos α} \end{matrix}

idő alatt ér át a túlsó partra, és

\begin{matrix} s = (v - u sin α) t_{1} \end{matrix}

távolsággal az aranyrög alatt ér partot. Ezt az utat

\begin{matrix} t_{2} = \frac{s}{u} = D \frac{v - u sin α}{u^{2} cos α} \end{matrix}

idő alatt teszi meg. Így az aranyrög elérése az

α

szög függvényében összesen

\begin{matrix} t (α) = t_{1} + t_{2} = \frac{D}{u} \cdot \frac{v / u + 1 - sin α}{cos α} \end{matrix}

időt vesz igénybe. Ha

α

-t egy kicsi

Δ α

értékkel megváltoztatjuk,

t

is megváltozik, értéke

\begin{matrix} t (α + Δ α) = \frac{D}{u} \cdot \frac{v / u + 1 - sin α}{cos α} + \frac{D}{u} \cdot \frac{(v / u + 1) sin α - 1}{cos^{2} α} Δ α \end{matrix}

lesz. A levezetés során kihasználtuk, hogy kicsiny

Δ α

esetén

\begin{matrix} sin Δ α \approx Δ α és cos Δ α \approx 1, \end{matrix}

így

\begin{matrix} sin (α + Δ α) \approx sin α + Δ α cos α, \end{matrix}

illetve

\begin{matrix} cos (α + Δ α) \approx cos α - Δ α sin α, \end{matrix}

továbbá azt, hogy

\begin{matrix} {(1 - Δ α tg α)}^{- 1} \approx (1 + Δ α tg α), \end{matrix}

{(Δ α)}^{2}

nagyságrendű tagokat pedig elhanyagoltuk. (Ezek a közelítések annál jobbak, minél kisebb

Δ α

.) Ha

t (α)

minimális, akkor

t

értéke sem pozitív, sem negatív

Δ α

mellett nem csökkenhet, következésképpen

Δ α

együtthatója nulla kell legyen:

\begin{matrix} \frac{(v / u + 1) sin α - 1}{cos^{2} α} = 0, innen sin α = \frac{u}{v + u} . \end{matrix}

Eddigi számításunk csak akkor helyes, ha

v - u sin α \geq 0

. Ellenkező esetben

s

negatív lenne, azaz Joe az aranyrög ,,fölött'' érne partot. Ilyenkor

t_{2} = - s / u

-val kellene számolnunk, de ezt az esetet nem érdemes végigszámolni, mert nyilván időveszteség, ha Joe ,,túlevez'' az aranyrögön. Ekkor (tehát ha a

v \leq u sin α

) Joenak úgy érdemes eveznie, hogy az eredő sebessége merőleges legyen a folyó partvonalára. A két esetet elválasztó határesetben

\begin{matrix} v - u \frac{u}{v + u} = 0, azaz \frac{v}{u} = \frac{u}{v + u}, \end{matrix}

ahonnan

\begin{matrix} \frac{v}{u} = \frac{\sqrt[]{5} - 1}{2} \approx 0, 618. \end{matrix}

Ez éppen az aranymetszés nevezetes arányszáma.
A fenti eredményt a differenciálszámítás formális szabályainak alkalmazásával vagy az

\begin{matrix} f (α) = \frac{| R - sin α | + 1}{cos α} \end{matrix}

függvény (

R = v / u

) grafikus vizsgálatával is megkaphatjuk (2. ábra).

W. F.

Megjegyzés. A megoldás során természetesnek vettük, hogy Joe a vízben egyenes vonalban evez, és a szárazföldön is egyenes vonalban gyalogol. Ez utóbbi ‐ a legrövidebb idejű mozgásnál ‐ nyilván igaz (hiszen ,,két pont között legrövidebb út az egyenes''), az előbbi célszerűségét pedig a vízhez rögzített koordináta-rendszerben lehet a legkönnyebben belátni.