Feladat:	B.3423	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2001/szeptember, 354. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 2001/január: B.3423

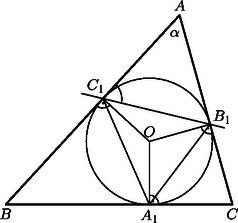
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a háromszög csúcsait és szögeit a szokásos módon $A$, $B$, $C$, illetve $\alpha$, $\beta$, $\gamma$-val, a beírt kör érintési pontjait $A_1$, $B_1$, $C_1$-gyel, középpontját pedig $O$-val (lásd az ábrát). Egy külső pontból egy körhöz húzott két érintő hossza egyenlő, ezért az $A{B}_1{C}_1$ háromszög egyenlő szárú. Az alapon fekvő szögek egyenlőek, tehát $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle A{B}_1{C}_1\sphericalangle =A{C}_1{B}_1\sphericalangle =}\\ \hfill {\displaystyle =\frac{{180}^{\circ }-B_{1}A{C}_1\sphericalangle }{2}={90}^{\circ }-\frac{\alpha }{2}\mathrm{.}}\end{array}}}\end{array}$ Vagyis $A{B}_1{C}_1\sphericalangle$ hegyesszög. Ez a szög a beírt kör rövidebbik $B_1{C}_1$ ívéhez tartozó érintőszárú kerületi szög, tehát megegyezik az ugyanehhez az ívhez tartozó közönséges kerületi szöggel, a $B_1{A}_1{C}_1\sphericalangle$-gel. Ezért ez utóbbi is hegyesszög. Ugyanígy látható be, hogy az $A_1{B}_1{C}_1$ háromszög másik két szöge is hegyesszög, vagyis a beírt körnek az oldalakon lévő érintési pontjai mindig hegyesszögű háromszöget alkotnak.   II. megoldás. Használjuk az I. megoldás jelöléseit. Mivel $O{B}_1\perp AC$ és $O{C}_1\perp AB$, azért a $B_1{C}_1$ egyenes elválasztja az $A$ és az $O$ pontokat. De $B_1{C}_1$ nyilván elválasztja az $A$ és az $A_1$ pontokat is, ezért $O$ és $A_1$ a $B_1{C}_1$ egyenesnek ugyanarra az oldalára esik. Vagyis $O$ benne van abban a $B_1{C}_1$ egyenes által meghatározott félsíkban, amelyikben az $A_1{B}_1{C}_1$ háromszög is elhelyezkedik. Ez nyilván igaz az $A_1{B}_1$ és az $A_1{C}_1$ egyenesek által meghatározott félsíkokra is. Tehát $O$ benne van a három félsík metszetében, azaz $O$ az $A_1{B}_1{C}_1$ háromszög belső pontja. Az $A_1{B}_1{C}_1$ háromszög köré írt kör éppen az $ABC$ háromszög beírt köre. Tehát az $A_1{B}_1{C}_1$ háromszög tartalmazza a köré írt kör középpontját. Ez viszont azt jelenti, hogy a háromszög hegyesszögű. Vagyis egy háromszög beírt körének az oldalakon lévő érintési pontjai nem alkothatnak tompaszögű háromszöget.