Kezdőlap


Feladat:	3444. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hamar Gergő
Füzet:	2002/január, 48 - 51. oldal		PDF \| MathML
Témakör(ök):	Egyéb merev test egyensúlya, Feladat
Hivatkozás(ok):	Feladatok: 2001/május: 3444. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a szuperellipszist kicsit kibillentjük az egyensúlyi helyzetéből, a tömegközéppontja eleinte emelkedik, vagyis távolodik az asztallap síkjától, majd egy maximális távolság elérése után ismét süllyedni kezd. A stabilitás határát (vagyis azt a szöget, amelynél kisebb kibillentés esetén még az eredeti helyzetbe tér vissza a test) a szuperellipszis azon $P$ pontja határozza meg, amelyik $e$ érintője a legmesszebb fekszik a szuperellipszis geometriai $(O)$ középpontjától (1. ábra).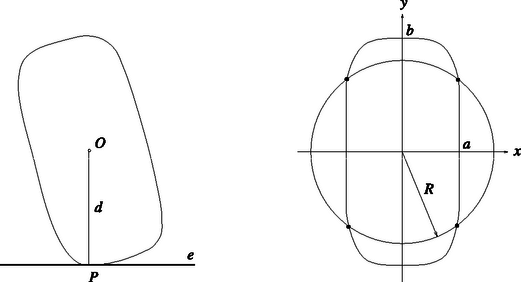

1. ábra 2. ábra

Vizsgáljuk meg, hogy egy

a

és

b

(

a < b

) féltengelyekkel rendelkező szuperellipszis és egy adott

R

sugarú kör hány pontban metszheti egymást (2. ábra). Ehhez meg kell oldanunk az

\begin{matrix} \frac{x^{4}}{a^{4}} + \frac{y^{4}}{b^{4}} = 1, x^{2} + y^{2} = R^{2} \end{matrix}

egyenletrendszert. A kör egyenletéből

y

-t kifejezve és a másik egyenletbe helyettesítve az

\begin{matrix} \frac{x^{4}}{a^{4}} + \frac{{(R^{2} - x^{2})}^{2}}{b^{4}} = 1 \end{matrix}

negyedfokú egyenletet kapjuk, amely az

x^{2} = u

helyettesítéssel másodfokúvá alakítható:

\begin{matrix} (a^{4} + b^{4}) \cdot u^{2} - 2 a^{4} R^{2} \cdot u + a^{4} (R^{4} - b^{4}) = 0. \end{matrix}

Innen

\begin{matrix} u = \frac{a^{2}}{a^{4} + b^{4}} [a^{2} R^{2} \pm b^{2} \sqrt[]{a^{4} + b^{4} - R^{4}}], \end{matrix}

ahonnan látható, hogy csak

\begin{matrix} R \leq R_{{max}_{}^{}} = \sqrt[4]{a^{4} + b^{4}} \end{matrix}

esetén létezik a szuperellipszisnek és a körnek valós metszéspontja. (

R

-nek alsó korlátja is van. Ha ugyanis

R < a

, akkor az egyenlet egyik gyöke

u_{1} = x^{2} < 0

lenne, a másik pedig

u_{2} > R^{2}

, azaz

y^{2} < 0

miatt zárná ki a valós metszéspontokat.)
Az

R

sugár maximuma azt jelzi, hogy a szuperellipszisnek egyetlen pontja sem lehet messzebb az origótól, mint

R_{{max}_{}^{}}

, és emiatt egyetlen érintője sem lehet távolabb az

O

ponttól, mint az

R = R_{{max}_{}^{}}

-nak megfelelő érintő.
Megtaláltuk tehát a stabilitás határának megfelelő

P

pontokat, és azok koordinátáit: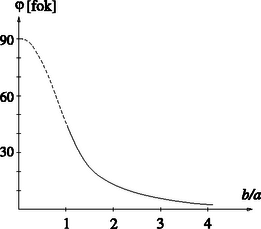

\begin{matrix} x_{P} = \pm \frac{a^{2}}{\sqrt[]{a^{4} + b^{4}}} R_{{max}_{}^{}}, és y_{P} = \pm \frac{b^{2}}{\sqrt[]{a^{4} + b^{4}}} R_{{max}_{}^{}}, \end{matrix}

illetve az ezeknek megfelelő maximális kibillentés szögét:

\begin{matrix} φ_{{max}_{}^{}} = arctg \frac{| x_{P} |}{| y_{P} |} = arctg \frac{a^{2}}{b^{2}} = arctg \frac{1}{k^{2}}, \end{matrix}

ahol

k = b / a

a ,,lapultsági arány''. Ezt a függvényt ábrázolva (3. ábra) látható, hogy ‐ a várakozásnak megfelelően ‐ minél lapultabb egy szuperellipszis, annál kisebb szögben billenthetjük ki a nagyobb tengelyét a függőleges helyzetből. (Jóllehet a fenti levezetés során feltételeztük, hogy

k > 1

, a kapott eredmény azonban

k \leq 1

esetén is érvényes, emiatt tüntettük fel a 3. ábrán a ,,fekvő helyzetű'' szuperellipszisek stabilitási szögeit is.)

3. ábra

Érdekes, hogy a ,,csúcsára'' állított szuperellipszis tetszőlegesen nagy

b / a

lapultsági arány mellett stabil egyensúlyi helyzetben van, magától nem borul fel, hiszen a kritikus

φ

szög nem nulla (jóllehet

b / a

növelésével

φ

egyre kisebbé válik)! Belátható, hogy ezzel a tulajdonsággal nem csak a feladatban szereplő alakú test, hanem minden

{| x / a |}^{n} + {| y / b |}^{n} = 1

egyenlettel leírt ,,hengeres test'' rendelkezik, amennyiben

n > 2

(G. P.)

II. megoldás. Az instabil egyensúlyi helyzetben ‐ ez felel meg a stabilitás határának ‐ a súlypont az szuperellipszis és az asztal érintési pontja ,,felett'' helyezkedik el, vagyis az érintő merőleges a középpontból az érintési pontba húzott sugárra. A görbe

\begin{matrix} b^{4} x^{4} + a^{4} y {(x)}^{4} = a^{4} b^{4} \end{matrix}

alakra hozott egyenletét

x

szerint deriválva (és kihasználva a közvetett függvény differenciálási szabályát) azt kapjuk, hogy

\begin{matrix} 4 b^{4} x^{3} + 4 a^{4} y^{3} \cdot y' = 0, azaz y' = - \frac{b^{4}}{a^{4}} \cdot \frac{x^{3}}{y^{3}}, \end{matrix}

amit a sugár és az érintő merőlegességének

y' = - x / y

feltételével összevetve a stabilitás határszögére a

\begin{matrix} tg φ = \frac{x}{y} = \frac{a^{2}}{b^{2}} = \frac{1}{k^{2}} \end{matrix}

feltétel adódik.

Hamar Gergő (Dombóvár, Illyés Gy. Gimn., 11. o.t.) dolgozata alapján

Megjegyzés. Említettük, hogy a hosszabb tengelyével függőlegesre állított szuperellipszis keresztmetszetű homogén henger tetszőlegesen nagy

b / a

arány mellett magától nem borul fel, egyensúlyi állapota elegendően kicsi kitérésekkel szemben stabil.
Naiv (és hibás) érveléssel ennek az állításnak éppen az ellenkezőjére lehet következtetni. Képzeljünk el egy adott méretarányú szuperellipszist, melynek tömegközéppontja

b

magasan van az asztal lapja fölött. Ha a szuperellipszis legmélyebb pontjában a görbületi sugár

r

, és a testet egy kicsit kibillentjük a szimmetrikus helyzetéből, akkor az

r

-nél alacsonyabban fekvő pontjai az asztal síkjától eltávolodnak, az

r

-nél magasabban fekvők viszont közelednek az asztalhoz. (Gondoljunk egy vízszintes úton haladó kerékpár kerekének küllőire. A tengely alatt éppen függőlegesen álló küllő egyes részei pályájuk legmélyebb pontján, a tengely feletti függőleges küllő darabkái pedig éppen a legmagasabb helyzetükben találhatók.) A stabilitás feltétele nyilván az, hogy

b < r

teljesüljön.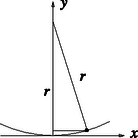

4. ábra

Tételezzük fel, hogy a csúcsára állított szuperellipszisünk valamilyen

a

és

b

féltengelyek esetén stabil egyensúlyban van. Növeljük meg

b

-t

N

-szeresére, ekkor az

r

görbületi sugár

N

-edrészére csökken. Ezt például úgy láthatjuk be, hogy a simulókört az asztallal való érintkezési pont közelében parabolával közelítjük, és ezen a parabolán hajtjuk végre az

y

tengely menti nyújtást. A 4. ábra jelöléseivel

\begin{matrix} x^{2} + {(r - y)}^{2} = r^{2}, tehát r = \frac{x^{2} + y^{2}}{2 y} \approx \frac{x^{2}}{2 y}, \end{matrix}

ahonnan látható, hogy

y

irányú

N

-szeres nyújtás hatására

r

N

-ed részére csökken. Ha

N

elegendően nagy, akkor

N b > r / N

fog teljesülni, az ilyen méretarányú test tehát instabil kell(ene) legyen.
Hol a hiba ebben a ,,levezetésben''? Ott, hogy a szuperellipszis görbületi sugara a tengelyeinek végpontjában nem véges érték, hanem ,,végtelen nagy''. Emiatt a ,,csúcsára állított'' test minden pontja távolodik az asztal síkjától, ha a testet kicsit kibillentjük, s ez a tulajdonság akkor sem változik meg, ha a szuperellipszist karcsúbbá tesszük, a

b / a

arányt megnöveljük. Ugyanez érvényes akkor is, ha a szuperellipszis egyenletében szereplő 4-es kitevőt valamely más

n > 2

értékre változtatjuk.

(G. P.)