Kezdőlap


Feladat:	3560. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	László Eszter , Nagy Róbert , Pálinkás Csaba , Paulin Dániel , Rakyta Péter , Sepsi Örs , Szabó Áron , Szilágyi Péter
Füzet:	2003/február, 119 - 121. oldal		PDF \| MathML
Témakör(ök):	Hajlítás, Feladat
Hivatkozás(ok):	Feladatok: 2002/október: 3560. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a pálca hosszát $L$ -lel, az útmutatásban szereplő arányossági tényezőt pedig $C$ -vel! Tekintsük először a kezdetben vízszintesen pálcát, amelynek egyik vége $G$ súly hatására $h$ távolsággal lehajlik. Közelítsük a meghajlított pálca alakját egyetlen $R$ sugarú körívvel!

Megjegyzés. Tudjuk ugyan, hogy a pálca görbülete (görbületi sugarának reciproka) a pálca egyes darabkáira ható forgatónyomatéktól függ, s emiatt a rögzítésnél a legnagyobb, a másik vége felé haladva egyre kisebbé válik, és a terhelésnél már nullára csökken. A görbület tehát nem lehet állandó, ennek ellenére ‐ a számítás egyszerűsítése érdekében ‐ mégis ezzel a durva közelítéssel élünk, hiszen nem pontos eredményt, hanem csak nagyságrendi becslést kívánunk kapni a keresett kritikus

F

terhelésre.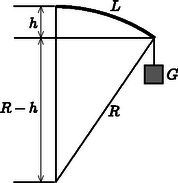

1. ábra

Ebben a közelítésben a görbületi sugár a Pitagorasz-tételből számítható (1. ábra):

\begin{matrix} R^{2} \approx {(R - h)}^{2} + L^{2}, \end{matrix}

ahonnan

h ≪ L

miatt

\begin{matrix} R \approx \frac{L^{2}}{2 h} \approx 50 m. \end{matrix}

(1)

(A kicsiny lehajlás miatt a meghajlított pálca vízszintes vetületének hosszát ugyancsak

L

-nek vettük.)
Vizsgáljuk most az energiaviszonyokat! Gondoljuk el, hogy a lehajlított pálca egyensúlyi állapota úgy jött létre, hogy saját erőnkkel szép lassan lenyomtuk a pálca végét (ehhez a lehajlással arányosan fokozatosan növekvő erőt kellett kifejtenünk), majd amikor elértük a megadott

h

értéket, ráakasztottuk a pálcára a

G

súlyt. Mivel az általunk kifejtett erő az elmozdulással arányosan nőtt, átlagosan a maximális erő felével számolhatunk, a végzett munkánk tehát

\begin{matrix} W = \frac{F_{{max}_{}^{}}}{2} h = \frac{G}{2} h . \end{matrix}

(2)

Ez a munka a pálca rugalmas energiáját növelte (a pálca saját súlyát elhanyagoljuk), tehát

\begin{matrix} W = C \frac{L}{R^{2}}, \end{matrix}

(3)

amiből (1) és (2) felhasználásával az arányossági tényezőre

\begin{matrix} C = \frac{G}{2} h \cdot \frac{R^{2}}{L} = \frac{G L^{3}}{8 h} = 125 J\cdotm \end{matrix}

adódik.

Megjegyzés. Ugyanerre az eredményre jutunk, ha a pálcából és a rá akasztott

G

súlyból álló rendszer energiáját vizsgáljuk a pálca

x

lehajlásának függvényében. Egyensúlyi állapotban az összenergia (ami

x

másodfokú függvényével közelíthető) minimális. Ha viszont a pálca rugalmas energiáját a nehezék helyzeti energiájának csökkenésével tesszük egyenlővé, egy kettes faktorban eltérő, hibás eredményt kapunk!

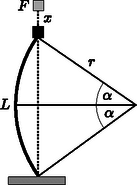2. ábra

Tekintsük most a függőlegesen terhelt pálcát. Képzeljük el, hogy a pálca tetejére

F

nagyságú súlyt helyeztünk, amelynek hatására a pálca a 2. ábrán látható módon meghajlik. Ez nyilván csak akkor következhet be, ha a teher helyzeti energiájának csökkenése fedezi a pálca rugalmas energiájának növekedését. A pálca alakját ismét egyetlen körívvel közelítjük, melynek sugarát

r

-rel jelöljük. (Természetesen

r

és a korábban szereplő

R

nem egyenlő!) Az ábrán látható szög (radiánban mérve)

\begin{matrix} α = \frac{L}{2 r}, \end{matrix}

és mivel ez a szög kicsiny, érvényes rá a

\begin{matrix} sin α \approx α - \frac{1}{6} α^{3} \end{matrix}

közelítő összefüggés. (Ez a formula differenciálszámítás felhasználásával vezethető le, de numerikusan akár egy zsebszámológéppel is könnyen ellenőrizhető.)
A pálca rugalmas energiájának növekedése

\begin{matrix} Δ E_{1} = C \frac{L}{r^{2}}, \end{matrix}

a súly helyzeti energiájának csökkenése pedig

\begin{matrix} - Δ E_{2} = F \cdot x = F (2 r α - 2 r sin α) \approx 2 F r \frac{α^{3}}{6} = \frac{1}{24} \frac{F L^{3}}{r^{2}} . \end{matrix}

A pálca ,,spontán'' kihajlásának feltétele:

| Δ E_{2} | > Δ E_{1}

, azaz

\begin{matrix} \frac{1}{24} \frac{F L^{3}}{r^{2}} > C \frac{L}{r^{2}} . \end{matrix}

Ez a feltétel ‐

r

értékétől függetlenül ‐ mindig teljesül, ha

\begin{matrix} F > F_{kritikus} = 24 \frac{C}{L^{2}} = 3 G \frac{L}{h} \approx 3000 N. \end{matrix}

() Szabó Áron (Debrecen, Fazekas M. Gimn., 11. o.t.) dolgozata alapján

II. megoldás. Az egyik végén mereven befogott, másik végén súllyal terhelt vízszintes rúd (pálca) lehajlása (lásd pl. a Négyjegyű függvénytáblázatban a ,,Rugalmas alakváltozások''-nál) az I. megoldásban használt jelöléseket követve

\begin{matrix} h = \frac{1}{3} L^{3} E I G, \end{matrix}

ahol

E

a rúd anyagának Young-modulusa,

I

pedig a rúd vastagságától és a keresztmetszetének alakjától függő ún. másodrendű keresztmetszeti nyomatéka. Innen kifejezhetjük az

E I

szorzatot:

\begin{matrix} E I = \frac{L^{3} G}{3 h} . \end{matrix}

(4)

A függőlegesen terhelt rúd kritikus terhelése (az ún. Euler-féle kritikus érték)

\begin{matrix} F_{kritikus} = E I \frac{π^{2}}{L^{2}} . \end{matrix}

(5)

(Ez az összefüggés levezethető a rugalmas alakváltozások lineáris elméletéből, lásd pl. R. Feynman: Mai fizika, 7. kötet, vagy megtalálható a ,,Mechanika szakközépiskolások számára'', Tankönyvkiadó, 1972. tankönyvben.) Az

E I

állandó (4)-beli értékét (5)-be helyettesítve a kritikus terhelésre

\begin{matrix} F_{kritikus} = \frac{π^{2}}{3} G \frac{L}{h} \approx 3300 N. \end{matrix}

() László Eszter (Pécs, Leöwey Klára Gimn., 9. o.t.)

Megjegyzés. A II. megoldásban hivatkozott képletek a lineáris (a Hooke-törvényt követő) rugalmasságtani egyenletek pontos megoldásaként adódnak, míg az I. megoldás összefüggései ‐ a görbület állandóságának feltételezése miatt ‐ csak közelítő jellegűek. A számítás pontosságát úgy lehetne javítani, ha a pálca alakját több (mondjuk 2 vagy 3) különböző sugarú körívvel közelítenénk, és a rugalmas energiát szakaszonként számolnánk ki.
A ,,pontos'' megoldás szerint a vízszintesen befogott pálca alakja egy harmadfokú polinommal írható le, a függőlegesen terhelt pálca pedig (kicsiny kihajlások esetén) egy fél szinuszhullámmal adható meg. A kétféle tárgyalás pontossága egymással is összevethető, ha kihasználjuk, hogy az

E I

szorzat éppen a

C

együttható 2-szerese. Eszerint a vízszintes rúd lehajlásának az erő kiszámításánál a ,,helyes'' érték

4 / 3

-szorosát, a függőleges rúd esetében pedig

12 / π^{2}

-szeresét kaptuk, a két erő arányát pedig mindössze egy

9 / π^{2}

-es faktor, vagyis kb. 10 százalékos hibával kaptuk meg.
Meglepő, hogy az alkalmazott durva közelítés ‐ felsőbb matematikai módszerek alkalmazása nélkül ‐ milyen jó becslést ad a kérdéses kritikus terhelésre.

() (G. P.)