Kezdőlap


Feladat:	3545. fizika feladat	Korcsoport: -	Nehézségi fok: nehéz
Megoldó(k):	Hablicsek Márton , Paulin Dániel , Szilágyi Péter , Tarján Gábor
Füzet:	2003/február, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Egyéb optikai leképezés, Egyéb fénytörés, Feladat
Hivatkozás(ok):	Feladatok: 2002/szeptember: 3545. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a gömbök sugarát $R$ -rel, a víz (levegőre vonatkoztatott) törésmutatóját pedig $n_{v,l} = n$ -nel!
Ha elhanyagoljuk az akvárium falának vastagságát (a sugarához viszonyítva), akkor a képalkotást úgy tekinthetjük, mintha az egyik halacska egy víz-közegben lévő kétszerhomorú (bikonkáv) levegőlencsén keresztül nézné a másik halat. Hogyha a gömbök méretéhez viszonyítva a halak mérete kicsi, akkor elegendő a gömbök érintkezési pontja közelébe eső ,,lencserészlettel'' foglalkoznunk, és alkalmazhatjuk a vékony lencsékre érvényes formulákat. A lencsetörvény szerint

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{1}{f} = (n_{l,v} - 1) (\frac{1}{R_{1}} + \frac{1}{R_{2}}), \end{matrix}

ahol

\begin{matrix} n_{l,v} = \frac{1}{n_{v,l}} = \frac{1}{n} \approx \frac{3}{4} \end{matrix}

a levegőnek vízre vonatkoztatott törésmutatója,

R_{1} = R_{2} = - R

a homorú lencse határfelületeinek görbületi sugarai,

t = R

a (lencsétől mért) tárgytávolság,

k

pedig a keresett képtávolság.
Ezekkel az adatokkal

f = 2 R > 0

, tehát a homorú lencse ‐ az 1-nél kisebb relatív törésmutató miatt ‐ gyűjtőlencseként viselkedik, továbbá

k = - 2 R

, tehát virtuális kép keletkezik, a lencsétől olyan távolságban, amilyen messze az akvárium legtávolabbi pontja van. (Ez azonban nem jelenti azt, hogy az egyik halacska a másikat az akvárium túlsó falánál látja, hiszen a túlsó fal éppen fókusztávolságnyira van a levegőlencsétől, a képe tehát a ,,végtelenbe'' kerül.) A nagyítás 2-szeres, és a kép egyenes állású. Az elrendezés a gömbök érintkezési pontjára nézve szimmetrikus, tehát mindkét halacska a leírtaknak megfelelő módon látja a másikat.

() Paulin Dániel (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) és
Tarján Gábor (Szolnok, Verseghy F. Gimn., 12. o.t.) dolgozata alapján

II. megoldás. Tegyük fel, hogy az akvárium falvastagsága sokkal kisebb, mint az akvárium sugara; ekkor az üvegfal fénytörésével nem kell foglalkoznunk, tekinthetjük úgy, mintha a fény közvetlenül a vízből a levegőbe lépne ki és viszont.
Mivel a halak a két gömb érintkezési pontjának irányában (az ,,optikai tengely'' közvetlen közelében) látják egymást, elegendő az ehhez közel haladó fénysugarakra szorítkoznunk.

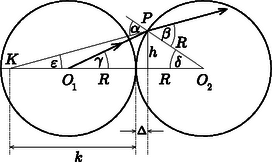
Tekintsük az egyik gömb

O_{1}

középpontjából kicsiny

γ

szögben kiinduló fénysugarat (lásd az áttekinthetőség miatt erősen eltorzított ábrát). Ez a fénysugár ‐ mivel a gömb sugarának irányában halad ‐ törés nélkül lép ki a levegőbe, a

P

pontban

α

beesési szöggel eléri a másik gömböt, ott megtörik, és a másik gömb

O_{2} P

sugarához képest

β

szögben halad tovább. A Snellius‐Descartes-törvény szerint (és a szögek kicsinységét is kihasználva)

\begin{matrix} \frac{sin α}{sin β} \approx \frac{α}{β} = n \approx \frac{4}{3} . \end{matrix}

(1)

Felhasználhatjuk továbbá, hogy egy háromszög külső szöge egyenlő a nem mellette levő belső szögek összegével. Az ábra jelöléseivel:

\begin{matrix} α = γ + δ, \end{matrix}

(2)

továbbá

\begin{matrix} β = δ + ε . \end{matrix}

(3)

Ezeket (1)-be helyettesítve adódik

\begin{matrix} γ + δ = n (δ + ε) . \end{matrix}

(4)

Fejezzük ki az itt előforduló szögeket az ábrán látható

h

távolsággal, kihasználva, hogy kicsiny szögek tangense a szöggel közelíthető, továbbá hogy

Δ ≪ R

\begin{matrix} ε \approx \frac{h}{R}, és γ \approx δ \approx \frac{h}{R} . \end{matrix}

Ezeket (4)-be helyettesítve kapjuk, hogy ‐ a vizsgált közelítésben ‐

h

értékétől függetlenül

k = \frac{n}{2 - n} R = 2 R

. Eszerint az

O_{1}

-ből kiinduló fénysugarak megtörésük után úgy haladnak tovább, mintha az optikai tengelyen a gömbök érintkezési pontjától

k

távolságra levő

K

pontból indultak volna ki.

K

-ban tehát az

O_{1}

pontban levő halacska virtuális képe jön létre. A kép mérete ‐ a kép- és tárgytávolság arányából ‐ kétszerese a tárgy méretének, és a kép egyenes állású.

() Szilágyi Péter (Debreceni Egyetem Kossuth L. Gyak. Gimn., 11. o.t.) és
Hablicsek Márton (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) dolgozata alapján