Kezdőlap


Feladat:	3304. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Buti András
Füzet:	2001/április, 247 - 249. oldal		PDF \| MathML
Témakör(ök):	Lineáris hőtágulás, Feladat
Hivatkozás(ok):	Feladatok: 2000/január: 3304. fizika feladat

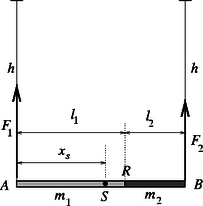
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a rudak eredeti hosszát $l_{i}$ -vel, a tömegüket $m_{i}$ -vel, lineáris hőtágulási együtthatójukat pedig $α_{i}$ -vel (ahol $i = 1$ a bal oldali, $i = 2$ pedig a jobb oldali rudra utal).
A hőmérséklet $Δ T$ nagyságú növekedtével az egyes fémrudak hossza $l_{i} α_{i} Δ T$ értékkel növekszik, a teljes hosszváltozás tehát

\begin{matrix} Δ L = Δ l_{1} + Δ l_{2} = (l_{1} α_{1} + l_{1} α_{1} Δ T . \end{matrix}

(1)

Ha ismernénk a rúd valamelyik pontjának, például az

S

tömegközéppontnak az elmozdulását, akkor már bármely más pontjának, így a ragasztás

R

helyének elmozdulását is meg tudnánk határozni.
A rudakra kezdetben csak függőleges erők hatnak, s ha a fonalak

h

hossza sokkal nagyobb, mint a rudaké, akkor a kicsit kitágult rudakra ható erők is majdnem pontosan függőleges irányúak. Ebből ‐ naívan ‐ arra következtethetünk, hogy a rendszer tömegközéppontja nem mozdul el. Ez azonban ‐ mint az alábbiakból kiderül ‐ hibás következtetés!
A fonalakat (hacsak a tömegközéppont nem esik éppen véletlenül a felezőpontra) különböző nagyságú erők feszítik. Nagyságuk az 1. ábrán látható

A

és

B

pontokra felírt forgatónyomatékok egyensúlyából határozhatjuk meg:

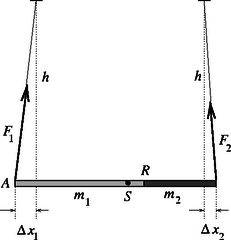
\begin{matrix} F_{1} = \frac{m_{1} (l_{2} + \frac{1}{2} l_{1}) + m_{2} \frac{1}{2} l_{2}}{l_{1} + l_{2}} g, F_{2} = \frac{m_{2} (l_{1} + \frac{1}{2} l_{2}) + m_{1} \frac{1}{2} l_{1}}{l_{1} + l_{2}} g . \end{matrix}

(2)

Az új (a rudak felmelegítése után kialakuló) egyensúlyi helyzetben a fonalak alsó vége valamekkora

Δ x_{1}

és

Δ x_{2}

távolsággal eltér az eredeti helyzettől (2. ábra), emiatt a fonalakban ható erőknek lesz vízszintes összetevője is. Mivel más vízszintes irányú erő nem hat, fenn kell álljon, hogy

\begin{matrix} F_{1} \cdot \frac{Δ x_{1}}{h} - F_{2} \cdot \frac{Δ x_{2}}{h} = 0. \end{matrix}

(3)

(Felhasználtuk, hogy a fonalak iránya csak kicsit tér el a függőlegestől, emiatt a fonálerők nagyságának változását, valamint a rúdnak a vízszintestől való eltérését nem kell figyelembe vennünk.) A (3) egyenlet

\begin{matrix} \frac{Δ x_{1}}{Δ x_{2}} = \frac{F_{2}}{F_{1}} \end{matrix}

(4)

alakba is írható, s ez jól mutatja, hogy az összeragasztott rúd végeinek elmozdulása

h

nagyságától függetlenül ‐ tehát tetszőlegesen hosszú fonalak esetén is ‐ mindig ugyanolyan arányban osztozik a teljes

\begin{matrix} Δ x_{1} = Δ x_{2} = Δ L \end{matrix}

(5)

hossznövekményen. A (2), (4) és (5) egyenletekből kiszámíthatjuk a rúd bal oldali

A

végpontjának elmozdulását:

\begin{matrix} Δ x_{1} = \frac{m_{2} (l_{1} + \frac{1}{2} l_{2}) + m_{1} \frac{1}{2} l_{1}}{(m_{1} + m_{2}) (l_{1} + l_{2})} (α_{1} l_{1} + α_{2} l_{2}) \cdot Δ T, \end{matrix}

(6)

majd ebből és a bal oldali rúd hosszának megváltozásából az

R

pont elmozdulását (a jobb fele mutató irányt véve pozitívnak):

\begin{matrix} Δ x_{R} = l_{1} α_{1} Δ T - x_{1} = \frac{(m_{1} l_{1} + m_{2} l_{2}) (α_{1} l_{1} - α_{2} l_{2}) + 2 l_{1} l_{2} (m_{1} α_{1} - m_{2} α_{2})}{2 (m_{1} + m_{2}) (l_{1} + l_{2})} Δ T . \end{matrix}

Ennek a kifejezésnek az előjele dönti el, hogy merrefelé mozdul el a két rúd érintkezési helye. Ha

\begin{matrix} \frac{α_{1}}{α_{2}} > \frac{l_{2}}{l_{1}} \cdot \frac{m_{1} l_{1} + m_{2} l_{2} + 2 m_{2} l_{1}}{m_{1} l_{1} + m_{2} l_{2} + 2 m_{1} l_{2}}, \end{matrix}

akkor az

R

pont jobbra mozdul el, ellenkező esetben pedig balra.

Buti András (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) dolgozatának felhasználásával

Megjegyzés. Bár a feladat nem kérdezte, érdemes kiszámítani a tömegközéppont elmozdulását is. Kezdetben a tömegközéppont a bal oldali rúdvégtől

\begin{matrix} x_{s} = \frac{m_{2} (l_{1} + \frac{1}{2} l_{2}) + m_{1} \frac{1}{2} l_{1}}{m_{1} + m_{2}} \end{matrix}

távol van, ennek a mennyiségnek a megváltozása a hőtágulás hatására:

\begin{matrix} Δ x_{s} = \frac{m_{2} (α_{1} l_{1} + \frac{1}{2} α_{2} l_{2}) + m_{1} \frac{1}{2} α_{1} l_{1}}{m_{1} + m_{2}} . \end{matrix}

A tömegközéppont elmozdulása jobb felé:

\begin{matrix} Δ x_{s} - Δ x_{1} = \frac{l_{1} l_{2}}{2 (l_{1} + l_{2})} (α_{1} - α_{2}) Δ T . \end{matrix}

Látható, hogy a tömegközéppont mindig a kisebb hőtágulási együtthatójú fémrúd irányába tolódik el, ha viszont a két anyag hőtágulás szempontjából egyformán viselkedik, akkor s tömegközéppont ‐ a méret- és tömegarányoktól függetlenül ‐ az eredeti helyén marad.