Kezdőlap


Feladat:	C.712	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2003/december, 535 - 537. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Trigonometriai azonosságok, Koszinusztétel alkalmazása, Hasonlósági transzformációk, C gyakorlat
Hivatkozás(ok):	Feladatok: 2003/március: C.712

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B$ oldalon $D$ az a pont, amelyre $A C D ∢ = α$ . Ekkor $C D B ∢$ az $A D C$ háromszögben külső szög, így $C D B ∢ = 2 α$ . Az $A D C$ és a $C D B$ háromszögek egyenlő szárúak, $C B = B D = 27$ és így $A D = A B - D B = 21 = D C$ (1. ábra).

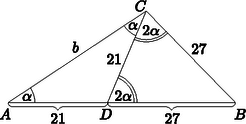1. ábra

C D B

háromszögben a koszinusztételt felírva

cos 2 α

kifejezhető:

\begin{matrix} cos 2 α = \frac{D C^{2} + D B^{2} - C B^{2}}{2 \cdot D C \cdot D B} = \frac{21^{2} + 27^{2} - 27^{2}}{2 \cdot 21 \cdot 27} = \frac{7}{18} . \end{matrix}

Írjuk fel a koszinusztételt az

A D C

háromszögben és használjuk fel, hogy

cos (180^{\circ} - 2 α) = - cos 2 α

\begin{matrix} \begin{matrix} b^{2} = A C^{2} & = & A D^{2} + D C^{2} - 2 \cdot A D \cdot D C \cdot cos (180^{\circ} - 2 α) = \\ = & 2 \cdot 21^{2} + 2 \cdot 21 \cdot 21 \cdot cos 2 α = 2 \cdot 21^{2} (1 + \frac{7}{18}) = \frac{2 \cdot 21^{2} \cdot 5^{2}}{2 \cdot 9} = 7^{2} \cdot 5^{2}, \end{matrix} \end{matrix}

ahonnan a

b

oldal hossza 35 egység.

Megjegyzés. Az 1. ábra alakzatához hasonló esetben létrejövő szakaszok között a Stewart-tétel néven ismert összefüggés áll fenn. Ha

D

A B

oldal tetszőleges pontja, akkor a 2. ábra betűzésével

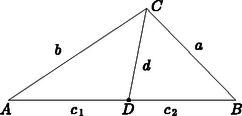\begin{matrix} c \cdot (d^{2} + c_{1} \cdot c_{2}) = a^{2} \cdot c_{1} + b^{2} \cdot c_{2} . \end{matrix}

2. ábra

II. megoldás. Rajzoljuk meg a

C

csúcsnál lévő

3 α

nagyságú szög szögharmadoló egyeneseit, messék ezek az

A B

oldalt a

D

, illetve

E

pontokban. Az előző megoldás szerint

A D = 21

D B = 27

, és

C E B ∢ = 3 α

(3. ábra).

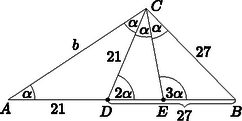3. ábra

Az ábrán két pár hasonló háromszög található:
(1)

A B C \sim C B E

, hiszen mindkettejükben van egy

α

és egy

3 α

nagyságú szög, továbbá
(2)

A E C \sim C E D

, hiszen mindkettejüknek van egy

α

és egy

2 α

nagyságú szöge.
Az első hasonlóságból

\frac{A C}{C E} = \frac{B C}{B E}

, ahonnan

A C = \frac{C E \cdot B C}{B E} = \frac{27 \cdot C E}{B E}

. A másodikból

\frac{C E}{A E} = \frac{D E}{C E}

, ahonnan

C E^{2} = A E \cdot D E

.
Felhasználva, hogy

A E = 21 + D E

és

B E = 27 - D E

, azt kapjuk, hogy

\begin{matrix} A C = \frac{27 \cdot \sqrt[]{(21 + D E) \cdot D E}}{27 - D E} . \end{matrix}

(1)

D E

szakasz hosszát a

B C D

háromszögből kaphatjuk meg a szögfelező tétel felhasználásával:

\begin{matrix} \frac{D E}{E B} = \frac{D E}{27 - D E} = \frac{D C}{C B} = \frac{21}{27}, ahonnan D E = \frac{189}{16}, \end{matrix}

(1)-be behelyettesítve

A C = 35

III. megoldás. Az

a

c

oldalakra írjuk fel a szinusztételt:

\frac{48}{27} = \frac{sin 3 α}{sin α}

. Az addíciós tétel felhasználásával:

\begin{matrix} \begin{matrix} \begin{matrix} sin 3 α & = sin (2 α + α) = sin 2 α \cdot cos α + cos 2 α \cdot sin α = \\ = 2 sin α \cdot cos^{2} α + cos^{2} α \cdot sin α - sin^{3} α = 3 cos^{2} α \cdot sin α - sin^{3} α . \end{matrix} \\ \frac{3 cos^{2} α \cdot sin α - sin^{3} α}{sin α} = \frac{48}{27} = \frac{16}{9} . \end{matrix} \end{matrix}

Egyszerűsíthetünk

sin α \neq 0

-val, így a négyzetes összefüggés felhasználásával a következő másodfokú egyenlethez jutunk:

36 cos^{2} α = 25

, innen

cos α = \pm \frac{5}{6}

. A

γ = 3 α

feltétel miatt

cos α

nem lehet negatív.
Ezután írjuk fel az

a

oldalra a koszinusztételt:

\begin{matrix} a^{2} = b^{2} + c^{2} - 2 b c \cdot cos α . \end{matrix}

Behelyettesítve az ismert értékeket:

\begin{matrix} 27^{2} = b^{2} + 48^{2} - 2 b \cdot 48 \cdot \frac{5}{6} . \end{matrix}

Elvégezve a műveleteket a

b^{2} - 80 b + 1575 = 0

másodfokú egyenlethez jutunk. Innen

b = 35

, illetve

b = 45

. Könnyű igazolni, hogy

b = 45

nem megoldása a feladatnak. Mivel

α

a

és

b

közül a kisebbikkel szemben fekvő szög, a szerkesztés során két háromszöget is kapunk, a

b = 45

esetén azonban nem teljesül a

γ = 3 α

kikötés.

Megjegyzés. Az utóbbi megoldás végén felmerült diszkussziós probléma elkerülhető, ha

cos α = \frac{5}{6}

meghatározását követően a

\begin{matrix} sin α = \sqrt[]{1 - cos^{2} α} = \frac{\sqrt[]{11}}{6} \end{matrix}

és a

\begin{matrix} sin β = sin (180^{\circ} - 4 α) = sin 4 α = 2 sin 2 α \cdot cos 2 α = 4 sin α \cdot cos α \cdot (2 cos^{2} α - 1) \end{matrix}

egyenletekre ismét a szinusztételt alkalmazzuk:

\begin{matrix} \frac{b}{27} = \frac{sin β}{sin α} = 4 \cdot cos α \cdot (2 cos^{2} α - 1) = 4 \cdot \frac{5}{6} \cdot \frac{14}{36}, \end{matrix}

ahonnan

\begin{matrix} b = 27 \cdot 4 \cdot \frac{5}{6} \cdot \frac{14}{36} = 35. \end{matrix}