Feladat: B.3643 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bereczki Péter ,  Birkner Tamás ,  Farkas Balázs ,  Farkas Csaba ,  Fekete László ,  Filus Tamás ,  Gidófalvy Kitti ,  Gombkötő Tamás ,  Gyarmati Ákos ,  Hartmann Zoltán ,  Hubai Tamás ,  Hülber Tímea ,  Jankó Zsuzsanna ,  Király Csaba ,  Komjáthy Júlia ,  Kormányos Balázs ,  Kurgyis Zsuzsanna ,  Lorántfy Bettina ,  Matyuska Ferenc ,  Mészáros Tamás ,  Nagy Péter ,  Nándori Péter ,  Papp Márton ,  Pesti Veronika ,  Rácz Judit ,  Salát Máté ,  Sziládi Tamás ,  Szilágyi Csaba ,  Szilvási Tibor ,  Udvari Balázs 
Füzet: 2003/október, 420 - 421. oldal  PDF  |  MathML 
Témakör(ök): Kocka, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 2003/május: B.3643

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Tekintsük azt a három gúlát, melyeknek csúcsa közös, megegyezik a kocka egyik csúcsával, alaplapjaik pedig a kocka adott csúcsát nem tartalmazó lapjai (1. ábra). Ez a három darab négyzet alapú gúla egybevágó, mert a testátló körüli 120∘-os forgatással egymásba vihetők, ezért a kockát három egybevágó részre osztják.

 

 
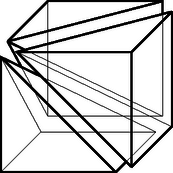1. ábra
 

Ha egy ilyen gúla alaplapja az ABCD négyzet, csúcsa pedig az A' pont, ahol AA' merőleges a négyzet síkjára, akkor azt az A', A és C csúcsokra illeszkedő sík két egybevágó tetraéderre osztja. Mindhárom gúlát ilyen módon kettévágva tehát a keresett felosztáshoz jutunk.
 

 
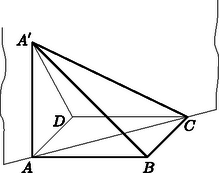2. ábra
 

() Fekete László (Révkomárom, Selye J. Gimn., 11. évf.) dolgozata alapján