|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Feltételezzük, hogy a felosztás véges sok paralelogrammából áll. A nyolcszög bármely két párhuzamos oldalára igaz, hogy paralelogrammák sorozata köti őket össze. Az egymásra merőleges oldalpárokat összekötő sorozatok egy paralelogrammában ,,metszik'' egymást. Megmutatjuk, hogy ez a paralelogramma téglalap.
Válasszuk ki a nyolcszög két szemközti oldalát, legyenek ezek és . Legyen egy olyan paralelogramma a felosztásból, amelynek valamely oldala illeszkedik az oldalra. -nek ezzel szemközti oldalát jelölje . Kell lennie olyan paralelogrammának is, amelynek egyik -vel jelölt oldala olyan, hogy -nek és -nek a metszete egy szakasz. -nek az -vel szemben lévő oldalát -vel jelölve megállapíthatjuk, hogy közelebb van a oldal egyeneséhez, mint . Folytassuk ezt az eljárást, amíg csak lehet.
Ilyen módon különböző paralelogrammáknak olyan sorozatához jutunk, hogy minden -re a paralelogramma oldalának és a paralelogramma oldalának közös része egy nem elfajuló szakasz, ami párhuzamos az , oldalakkal. Ha ezt a sorozatot már nem tudjuk folytatni (márpedig egy idő után nem tudjuk, hiszen csak véges sok, a felosztásban szereplő paralelogramma közül választhatunk) az csak úgy lehet, hogy az utolsó paralelogramma oldala illeszkedik a nyolcszög oldalára. Az , jelöléseket bevezetve, legyen esetén az szakasz felezőpontja. Ekkor az töröttvonal összeköti a nyolcszög és oldalának egy-egy pontját úgy, hogy az szakasz a végpontjaitól eltekintve végig a paralelogramma belsejében halad.
Legyen és a nyolcszögnek -ra és -re merőleges oldalpárja, és tekintsünk az előbbiek mintájára egy paralelogramma-sorozatot, ahol most a megfelelő oldalait és jelöli, és metszete a felezőpontú szakasz, és a töröttvonal összeköti a nyolcszög és oldalának egy-egy pontját úgy, hogy a szakasz a végpontjaitól eltekintve végig a paralelogramma belsejében halad.
A konstrukcióból adódik, hogy az és töröttvonalak a nyolcszög belsejében, egy pontban metszik egymást. Az és szakaszok nem metszhetik egymást, különben a és paralelogrammák egymásba nyúlóak lennének. Ezért a paralelogrammák közül valamelyiknek belső pontja; az általánosság megszorítása nélkül feltehetjük, hogy a belsejében helyezkedik el. Mivel egyben valamelyik -nek is pontja, és a paralelogrammák nem nyúlnak egymásba, ez csak úgy lehetséges, ha megegyezik -vel. Ekkor azonban olyan paralelogramma, melynek oldalai rendre az , , , szakaszokkal párhuzamosak. A felosztásban szereplő paralelogramma tehát téglalap.
() Bereczki Péter (Szeged, Ságvári Gimn., 9. évf.) és
Tóth János (Békéscsaba, Rózsa Ferenc Gimn., 12. évf.) megoldása alapján |
Megjegyzések. 1. Természetesen van még legalább egy másik téglalap is a felbontásban, hiszen a nyolcszög megmaradt négy oldalára is alkalmazható a megoldás gondolatmenete.
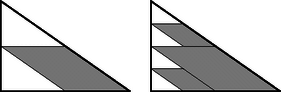
2. Ha a paralelogrammák száma nem véges, akkor a feladat állítása nem igaz:
Daraboljuk fel ehhez háromszögekre a nyolcszöget. Minden ilyen háromszögbe írjunk az ábra szerint paralelogrammákat.
Ekkor ‐ az eljárást a végtelenségig folytatva ‐ a nyolcszöget olyan paralelogrammákra oszthatjuk fel, amelyek nyilvánvalóan nem téglalapok.
II. megoldás. A megoldás során összeszámoljuk a paralelogrammák hegyesszögű, valamint tompaszögű csúcsait. Azt tapasztaljuk, hogy ha nincsenek derékszögű csúcsok, akkor több hegyesszögű csúcs van, mint tompaszögű; ez nyilván ellentmondás, hiszen minden egyes paralelogrammának azonos számú hegyesszögű és tompaszögű csúcsa van.
A felbontásban szereplő bármely paralelogramma-oldal párhuzamos a nyolcszög valamelyik oldalával. Tetszőleges oldalból kiindulva lépjünk a paralelogramma szemben levő oldalára, majd a továbbira. Így a párhuzamos oldalak egymásutánját kapjuk, amelynek utolsó eleme a nyolcszög valamelyik oldala.
Tegyük fel, hogy a paralelogrammák között nincs téglalap. Ekkor csak kétféle szöge lehet a paralelogrammáknak: vagy . Így minden paralelogrammának két -os hegyes- és két -os tompaszöge van.
Számoljuk össze paralelogramma-csúcsonként, hogy az egyes szögekből mennyit találunk.
| I.) | a nyolcszög belső pontjaiban: |
| 2.) | 5 hegyes, 1 tompa, vagy |
Ezért minden belső csúcsban legalább annyi hegyesszög van, mint tompa.
| II.) | a nyolcszög határán lévő csúcsokban a különböző tulajdonságú szögeket paralelogrammánként számoljuk össze aszerint, hogy a paralelogramma és a nyolcszög határának közös része |
| 4.) | a paralelogramma egy teljes oldala: 1 hegyes, 1 tompa; |
| 5.) | a paralelogramma két teljes szemközti oldala: 2 hegyes, 2 tompa; |
| 6.) | a paralelogramma két teljes szomszédos oldala (ekkor van közös csúcsuk is): 2 hegyes, 1 tompa; |
| 7.) | a paralelogramma egyik csúcsa: 1 hegyes, hiszen tompaszög esetén e csúcs körül még két szögtartomány keletkezik, amelyek mindegyike kisebb, mint , ezért nem lenne lefedhető. |
Látható, hogy mindegyik esetben legalább annyi hegyesszög van, mint tompaszög, és ha a nyolcszög egy csúcsánál a 6., vagy a 7. eset valósul meg, akkor biztosan több hegyesszög keletkezik, mint tompa. Nem valósulhat meg minden csúcsnál a 4. eset, hiszen két, a nyolcszög egy-egy oldalához támaszkodó -os szög között marad egy ugyancsak -os szögtartomány, ami csak a 7. esethez tartozó módon fedhető le.
Összesen tehát több hegyesszög lesz, mint tompaszög, ami ellentmondás, hiszen a számuk egyenlő.
| () Pallos Péter (Fazekas M. Főv. Gyak. Gimn., 12. évf.) megoldása alapján |
|
 PDF |
PDF |  MathML
MathML