Feladat: B.3568 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Backhausz Ágnes ,  Baráth Géza ,  Bartha Ferenc ,  Bérczi Kristóf ,  Bereczky Péter ,  Birkner Tamás ,  Czank Tamás ,  Deák Péter ,  Hubai Tamás ,  Jelitai Kálmán ,  Komjáthy Júlia ,  Mánfay Máté ,  Pongrácz András ,  Ruppert László Gábor ,  Salát Máté ,  Sándor Nóra Katalin ,  Seres Gyula ,  Simon Balázs ,  Sipos Kinga ,  Szabó Botond ,  Szilvási Tibor ,  Tábor Áron ,  Torma Róbert ,  Tölgyesi Csaba ,  Vass Márton 
Füzet: 2003/május, 277 - 281. oldal  PDF  |  MathML 
Témakör(ök): Trigonometrikus egyenlőtlenségek, Síkgeometriai bizonyítások, Mértani sorozat, Függvényvizsgálat, Feladat
Hivatkozás(ok):Feladatok: 2002/szeptember: B.3568

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A cos2kx függvények mindegyikének periódusa a 2π, így elegendő a megoldásokat a [0;2π) intervallumon keresni. Másfelől

cos2kx=cos(2k(2π-x)),
így föltehető, hogy α∈[0;π].
A keresett halmaz helyett vizsgáljuk annak komplementerét, legyen H a [0;π] intervallum azon részhalmaza, amelynek x elemeire van olyan k, amelyre cos2kx>0. E halmaz meghatározásakor fölhasználjuk, hogy a cosmx függvény legkisebb periódusa 2πm. Hívjunk egy 2πm hosszúságú intervallumot a cosmx függvény tiszta periódusának, ha az intervallum kezdőpontjában 1 a függvény értéke. Ekkor cosmx minden tiszta periódusának első és utolsó félig nyílt negyedében pozitív (1. ábra).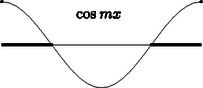
 
 

1. ábra
 

Így cosx>0, ha 0≤x<π2, ezért [0;π2)⊂H. Vegyük észre, hogy ez az intervallum éppen a cos4x függvény egy tiszta periódusa, emiatt az ehhez közvetlenül csatlakozó tiszta periódus alulról zárt első negyedén cos4x pozitív (2. ábra): 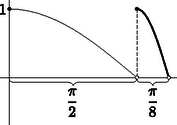[0;π2+π8)⊂H.
 
 

2. ábra
 

Így haladva a Hk=[0;π2+π8+...+π2⋅4k)⊂H intervallumok sorozatát kapjuk. A k-adik lépést megelőző növekmények mindegyike egész számú többszöröse a cos4kx függvény periódusának, tehát a Hk-1 intervallum végpontjában e függvény tiszta periódusa kezdődik. A k-adik lépésben tehát az intervallum ennek első negyedével, egy 14⋅2π4k hosszúságú felülről nyílt szakasszal bővül.
A Hk intervallumok fölső végpontjai egy mértani sor részletösszegei, ennek első tagja π2, hányadosa 14, így a sor konvergens és az összege π2⋅11-14=2π3.
Ez azt jelenti, hogy ha 0≤x<2π3, akkor van olyan k≥0, amelyre cos4kx pozitív.
Hasonlóan kapjuk a 2 páratlan kitevőjű hatványaira a cos(2⋅4kx) függvények egymáshoz csatlakozó tiszta periódusainak utolsó negyedét figyelembe véve, π végpontú intervallumok alulról bővülő sorozatát. A cos2x periódusa π, tehát a függvény a [0;π] tiszta periódus utolsó, alulról nyílt negyedében pozitív. Ennek az intervallumnak az alsó végpontja, π-π4 a cos8x egy tiszta periódusának a végpontja. Ennek a tiszta periódusnak az utolsó, π16 hosszúságú negyedén tehát cos8x pozitív. Így haladva a π végpontú intervallum hosszára adódó mértani sor első tagja π4, hányadosa 14, a sor összege az előbbi összeg fele, π3. Ha tehát π-π3<x≤π, akkor van olyan k≥0, amelyre cos(2⋅4kx) pozitív.
Eszerint [0;2π3)∪(2π3;π]⊂H, a [0;π] egyetlen szóbajövő eleme α=2π3. Ekkor cosα=-0,5 és cos2α=2cos2α-1 miatt cos2nα=cosα=-0,5 minden pozitív egész n-re. Így a [0;π] intervallumban α=2π3, a [0;2π) intervallumban ezen kívül α=2π-2π3=4π3, a további megoldások pedig: 2π3+2mπ, illetve 4π3+2nπ, ahol n és m tetszőleges egész számok.
() Tölgyesi Csaba (Kecskemét, Bányai Júlia Gimn., 12. évf.)

 

Megjegyzés. A helyes megoldások nagy része általában abból indult ki, hogy egy adott α szögre pontosan akkor teljesül a feltétel, ha minden k≥0 egészre van olyan m egész szám, hogy
(2m+1)π-π2≤2kα≤(2m+1)π+π2.(*)
Ha k=0, akkor ez a π2≤α≤3π2 feltételt jelenti, amit az előző megoldás szerint most is föltehető 0≤α<π korlát az I1=[π2;π] intervallumra szűkít. Innen 2α-ra egy π hosszúságú intervallumot kapunk: π≤2α<2π. A (*)-beli π hosszúságú intervallumok közül ezzel pontosan egynek, az m=0 esetén adódó [π2;3π2] intervallumnak nem üres a metszete. A két intervallum közös része [π;3π2], így α-ra egy π4 hosszúságú intervallum, az előző intervallum ,,alsó fele'' adódik: I2=[π2;3π4]=[2π4;3π4].
Ugyanígy haladhatunk tovább. Az α szögre a k-adik lépésben kapott
Ik=[nπ2k;(n+1)π2k]
intervallumot 2k-szorosára nagyítva kapjuk, hogy nπ≤2kα≤(n+1)π. Ezt a (*) intervallumok közül ismét pontosan egy metszi, a közös rész egy π2 hosszúságú intervallum, amelyet 2k+1-szeresére kicsinyítve kapjuk Ik+1-et, az előbbi Ik intervallum valamelyik felét. Hogy ez az alsó, vagy pedig a fölső, az attól függ, hogy n páratlan-e, vagy páros. A megoldáshoz azt kellett megmutatni, hogy ez lépésenként váltakozik ‐ ez általában teljes indukcióval történt ‐ és így az egymásba skatulyázott intervallumok közös részeként adódik α=2π3. A következő megoldás elegánsan kerüli el a fenti bonyodalmakat.
 
II. megoldás. Keressük a [0;2π)-beli megoldásokat α=d⋅2π alakban, ahol 0≤d<1. Ekkor 2α=2d⋅2π, tehát cos2α=cos({2d}⋅2π) és általában, ha dk={2kd}, akkor cos2kα=cos(dk⋅2π). A törtrész definíciója szerint dk⋅2π éppen 2kα maradéka 2π-vel osztva.
Ha 0≤φ<2π, akkor cosφ≤0 pontosan akkor teljesül, ha π2≤φ≤3π2, ami a dk együtthatókra nézve azt követeli meg, hogy
14≤dk≤34(1)
teljesüljön minden k≥0 egész számra.
Maguk a dk együtthatók természetes módon adódnak, ha a d kettes számrendszerbeli alakjából indulunk ki. Legyen d=0,x1x2x3... a d kettedes- vagy másképpen diadikus tört alakja. Az egyes jegyek értéke tehát 0 vagy 1. (A véges diadikus törteknek kétféle alakját is megengedjük, az adott helyiértéktől kezdődően azonosan nulla törteken kívül azokat is, amelyekben egy adott helyiértékkel kezdődően minden jegy 1-es.) Ekkor a 2-vel való szorzás eggyel jobbra lépteti a ,,kettedesvesszőt'', 2d=x1,x2x3..., az egész rész leválasztása pedig ezután törli az első jegyet: {2d}=0,x2x3x4.... Kettes számrendszerben 14=0,01 és 34=0,11, tehát kettes számrendszerben (1) azt jelenti, hogy minden k≥0 egész számra teljesülnie kell, hogy
0,01≤0,xkxk+1xk+2...≤0,11.(2)
Azt állítjuk, hogy ez pontosan akkor igaz, ha d-nek nincsenek egyenlő szomszédos jegyei, bármely két szomszédos helyiértéken 01 vagy 10 áll.
Ha ugyanis d=0,x1x2x3... tartalmaz valahol két szomszédos 0-t, valamilyen k-ra xk=xk+1=0, akkor 0,01≤dk=0,00xk+2xk+3... miatt a (k+2)-edik helyiértékkel kezdődően minden jegy 1-es és így dk+2=0,111...=1>34.
Hasonlóan, két szomszédos 1-es 0,11xk+2xk+3...=dk≤0,11 miatt azt jelentené, hogy a (k+2)-edik helyiértékkel kezdődően minden jegy 0 és így dk+2=0,000...=0<14.
A talált feltétel alapján d első jegye egyértelműen határozza meg a többit. Ha x1=0, akkor d'=0,0101...=0,01¯=13, ha pedig x1=1, akkor d''=0,1010...=0,10¯=23.
Erre a két számra nyilvánvalóan teljesül (2), így a feladatnak két megoldása van a [0;2π) intervallumon: α'=13⋅2π és α''=23⋅2π. A periodicitást figyelembe véve pedig α=2π3+2nπ, vagy pedig α=4π3+2nπ.
() Bereczky Péter(SZTE Ságvári Endre Gyakorló Gimnázium, 10. évf.)

 
III. megoldás. Ebben a megoldásban α helyett cosα értékét határozzuk meg. Ismeretes, hogy cos2α=2cos2α-1, így ha cosα=b, akkor cos2α=2b2-1=f(b).
Azokat a b∈[-1;1] értékeket keressük, amelyekre a
b1=b,bk+1=f(bk)(*)
sorozat elemei nem pozitívak.
 
 

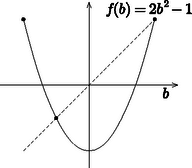3. ábra
 

Az f függvény a [-1;1] intervallumot ,,kétszeresen'' képezi le önmagára (3. ábra), két fixpontja van, f(1)=1 és f(-0,5)=-0,5. Innen nyomban adódik, hogy ha b1=-0,5; akkor a bk sorozat állandó és így minden tagja negatív, ez az érték tehát megfelelő. Azt állítjuk, hogy minden más kezdőértékre a (*) sorozat tagjai között van pozitív szám. Legyen tehát 0≥b≠-0,5. Egyszerű algebrai átalakítással
f(b)+0,5=2(b2-0,25)=(2b-1)(b+0,5).(3)
Innen kiolvasható, hogy ha b<0 és így |2b-1|>1, akkor |f(b)+0,5|>|b+0,5|, a sorozat tagjai távolodnak -0,5-től. Ebből még általában nem következik, hogy a bn sorozat feltétlenül kilép egy adott intervallumból. Ehhez olyan becslésre volna szükség, ahol a távolodás mértéke nem függ a b értékétől. Ilyen becslést kaphatunk, ha a sorozat három szomszédos tagját vesszük figyelembe.
Először is jegyezzük meg, hogy (3)-ból következik, hogy ha 0≥b≠-0,5; akkor f(b) sem lehet -0,5. Most (2b-1) negatív, ezért a nullától különböző b+0,5 és f(b)+0,5 értékek (3) szerint ellenkező előjelűek. Ha még f(b)≤0 is teljesül, akkor mivel -0,5 elválasztja b-t és f(b)-t, |2b-1| és |2f(b)-1| közül a nagyobbik legalább 1,5. Mivel a kisebbik is legalább 1, azért
(2f(b)-1)(2b-1)≥(0-1)(-0,5-1)=1,5.
Írjunk (3)-ban b helyére f(b)-t, majd használjuk fel ismét (3)-at:
f(f(b))+0,5=(2f(b)-1)(f(b)+0,5)=(2f(b)-1)(2b-1)(b+0,5).(4)

A fentiek szerint ha 0≥b≠-0,5 és f(b)≤0, akkor
|f(f(b))+0,5|≥1,5⋅|b+0,5|.
Azt kaptuk, hogy ha b1≠-0,5; akkor ameddig a bk sorozat elemei nem pozitívak, addig egyikük sem lehet -0,5; másrészt bk+2 legalább másfélszer olyan messze van -0,5-től, mint bk. Ha tehát b1≠-0,5; akkor a bk sorozat elemei nem lehetnek valamennyien a [-1;0] intervallumban. Mivel pedig tetszőleges b1∈[-1;1] kezdőértékre a sorozat minden eleme a [-1;1] intervallumban van, azért a sorozatnak ilyenkor van pozitív eleme.
Végül ha b1=cosα=-0,5; akkor α=±2π3+2nπ, ahol n tetszőleges egész szám.
() Hubai Tamás (Budapest, Fazekas Mihály Gimn., 11. évf.) dolgozata nyomán