Feladat: B.3586 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Jelitai Kálmán 
Füzet: 2003/április, 222 - 223. oldal  PDF  |  MathML 
Témakör(ök): Egyenletek grafikus megoldása, Logaritmusos egyenletek, Paraméteres egyenletek, Feladat
Hivatkozás(ok):Feladatok: 2002/november: B.3586

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Az (1) egyenlet akkor értelmes, ha ax>0 és x+1>0. Ha a>0, akkor ez a pozitív számokra teljesül, ha a=0, akkor nincs ilyen szám, ha pedig a<0, akkor -1<x<0 az értelmezési tartomány. Jelölje ezt az a-tól függő halmazt Ta.
Ha x∈Ta, akkor 2lg(x+1)=lg(x+1)2, ahonnan az ax=(x+1)2 egyenletet kapjuk, amit rendezve

x2+(2-a)x+1=0.(2)
A két egyenlet, (1) és (2) csak a Ta halmazon ekvivalens; ha a (2) egyenletet a valós számok halmazán vizsgáljuk ‐ ami kényelmesebb ‐, akkor általában bővebb megoldáshalmazt kapunk. Az a paraméternek azokat az értékeit kell megtalálnunk, amikor a (2) egyenletnek egyetlen valós gyöke van a Ta halmazon. Ez kétféleképpen lehetséges: a másodfokú (2)-nek is egyetlen gyöke van és ez eleme Ta-nak is, vagy pedig (2)-nek két gyöke van ugyan, de közülük csak az egyik van ott a Ta halmazban. (Erről az utóbbi lehetőségről igen sokan megfeledkeztek.)
Az első esetben (2) diszkriminánsa, D=(2-a)2-4=a(a-4)=0. Ha a=0, akkor Ta üres, (1)-nek nincs megoldása. Ha a=4, akkor Ta a pozitív számok halmaza, (2) bal oldala pedig (x-1)2, az egyetlen gyök x=1, ami valóban az (1) egyenlet egyetlen megoldása.
Vizsgáljuk meg a második lehetőséget: ekkor (2)-nek két megoldása van, ami pontosan akkor teljesül, ha D=a(a-4)>0, azaz a>4 vagy a<0. Legyenek x1<x2 a (2) gyökei. A gyökök és együtthatók összefüggése szerint x1x2=1, a két gyök tehát azonos előjelű. Nem lehet tehát pontosan az egyikük pozitív, így az a>4 esetben, amikor Ta a pozitív számok halmaza, az (1) egyenletnek nem lehet egyetlen gyöke. (Mivel x1+x2=a-2>0, most mindkét gyök pozitív, így az (1) egyenletnek ekkor két gyöke van.)
Ha a<0, akkor a gyökök összege, x1+x2=a-2<0, a két azonos előjelű gyök negatív. Az (1) egyenletnek ezúttal pontosan akkor van egy gyöke, ha -1 ,,elválasztja'' a két negatív gyököt, a kisebbik nincs a Ta halmazban. Ez pedig most teljesül, hiszen a két negatív gyök szorzata 1 és nem egyenlők. Ha tehát a negatív, akkor a (2) egyenlet két valós gyöke közül a nagyobbik lesz gyöke az (1) egyenletnek is.
Az (1) egyenletnek tehát akkor van pontosan egy valós gyöke, ha a=4 vagy a<0.
() Jelitai Kálmán (Budapest, Szent István Gimn., 12. évf.) dolgozata nyomán

 
Megjegyzések. 1. Sok hibás dolgozat érkezett. A tipikus hiba a két egyenlet ekvivalenciájának föltételezése volt, a szerzők a diszkrimináns nulla értékeinek vizsgálatára szűkítették a feladatot.
2. A helyes megoldások általában a másodfokú egyenlet megoldóképletéből adódó formulákat használták a gyökök vizsgálatára. A gyökök összege és szorzata alapján sok kérdés gyorsabban válaszolható meg, hiszen a ViŠte-formulák szerkezete lényegesen egyszerűbb.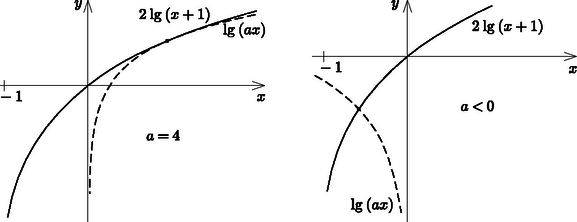
 
 

3. Gyorsabban célhoz érünk és a feladat szerkezete is világos lesz, ha grafikusan oldjuk meg a feladatot. Az ábrák az egyenlet két oldalán álló függvényeket ábrázolják a Ta halmazon az a>0, illetve az a<0 esetben. A jólismert grafikonokról azonnal leolvasható, hogy az első esetben a (2) egyenlet diszkriminánsa az (1) egyenlet viselkedését is a szokott módon jellemzi, illetve hogy ha a<0, akkor az (1) egyenletnek pontosan egy megoldása van.