Feladat: B.3578 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Birkus Róbert 
Füzet: 2003/március, 151 - 152. oldal  PDF  |  MathML 
Témakör(ök): Helyvektorok, Pont és egyenes távolsága, Térgeometriai számítások trigonometria nélkül, Pitagorasz-tétel alkalmazásai, Feladat
Hivatkozás(ok):Feladatok: 2002/október: B.3578

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy az A csúcs legyen az origó, az x, y, z tengelyek illeszkedjenek rendre a B, D, E pontokra, az egységet pedig válasszuk a kocka élhossza egytizedének. Ekkor az egyes pontok koordinátái: B(10;0;0), D(0;10;0), M(5;5;0), E(0;0;10).
A P pont pontosan akkor van rajta az AB, a Q pont pedig az EM egyenesen, ha léteznek olyan t, illetve s valós számok, melyekre

AP→=t⋅AB→,illetveAQ→=AE→+s⋅EM→.
Tehát a P és Q pontok koordinátái a t és s paraméterek segítségével kifejezve: P(10t;0;0), Q(5s;5s;10-10s). Tehát
PQ2=(10t-5s)2+(5s)2+(10-10s)2.

Ismert, hogy a két egyenes távolsága megegyezik a PQ távolságok minimumával. Rögzített s érték esetén PQ nyilván akkor a legkisebb, ha 10t=5s, azaz ha t=s/2. Ebben az esetben
PQ2=(5s)2+(10-10s)2=(55s-45)2+20.
Ez a kifejezés akkor minimális, ha s=0,8, vagyis a PQ távolság akkor a legkisebb, ha s=0,8 és t=0,4. Ekkor a P, illetve a Q pont koordinátái: P(4;0;0), Q(4;4;2).
A P pont tehát az a pont, amely az AB szakaszt 2:3 arányban osztja, Q pedig az ME szakaszt 1:4 arányban osztó pont.
() Birkus Róbert, Galánta, Kodály Z. Gimn., 11. évf. dolgozata alapján

 
II. megoldás. Ha az AD él felezőpontját N-nel jelöljük, akkor az AB egyenes nyilván párhuzamos az E, M és N pontokra illeszkedő S síkkal. Az AB egyenes merőleges vetülete S-en egy olyan e egyenes, mely AB-vel párhuzamos és áthalad az A pont EN egyenesre eső A' merőleges vetületén, hiszen az AEN sík merőleges az S síkra és az AB egyenesre is (1. ábra). Az AB él hosszát 10 egységnyinek tekintve AN=5, és a Pitagorasz-tétel alapján EN=55, valamint EM=56. Az AEN derékszögű háromszögben (2. ábra) a befogótétel szerint AN2=EN⋅A'N, tehát
A'N=52(55)=5,
és ezért EA'=45.
 
 

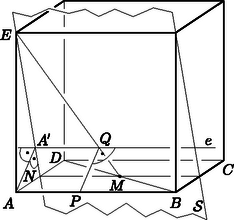1. ábra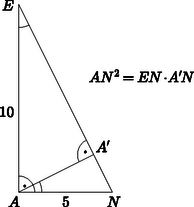
 

 
 

2. ábra
 

Ismert, hogy a PQ távolság pontosan akkor egyezik meg az AB és EM egyenesek távolságával, ha PQ merőleges mindkét egyenesre. Ezért a Q pont éppen az e egyenes EM egyenessel alkotott metszéspontja, P pedig Q merőleges vetülete az AB egyenesre. Az ENM és EA'Q derékszögű háromszögek középpontosan hasonlóak, ezért
EQ=(EA'EN)⋅EM=46ésA'Q=(EA'EN)⋅NM=4.

A Q pont tehát az EM szakaszt 4:1 arányban osztó pont, P pedig az AB szakaszt 2:3 arányban osztja, mert az APQA' négyszög téglalap, tehát
AP=A'Q=4.