Feladat: 2002. évi Kürschák matematikaverseny 1. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Harangi Viktor ,  Rácz Béla András 
Füzet: 2003/február, 67 - 71. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Körülírt kör középpontja, Magasságpont, Beírt kör középpontja, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 2003/február: 2002. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A K, O, M pontok a háromszög belsejében helyezkednek el. Ha a csúcsokat A, B, C, a megfelelő szögeket α, β, γ jelöli, akkor BAM∢=90∘-β=CAO∢. Itt a második egyenlőség abból következik, hogy az AOC egyenlő szárú háromszögben a kerületi és középponti szögek tétele miatt AOC∢=2β. Mivel az AK félegyenes felezi a BAC szöget, megállapíthatjuk, hogy az AM és AO félegyenesek az AK félegyenesre szimmetrikusan helyezkednek el. A három félegyenes nem eshet egybe (különben a háromszög egyenlő szárú lenne). Azt kaptuk tehát, hogy a KM és KO szakaszok az A csúcsból ugyanolyan szög alatt látszanak, továbbá az AK egyenes elválasztja az M és O pontokat. Ez az állítás természetesen akkor is igaz, ha A helyébe a háromszög B vagy C csúcsát írjuk.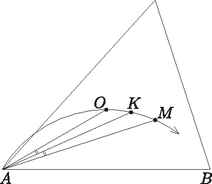
Tegyük fel most, hogy az A, M, K, O pontok egy körön helyezkednek el. A kerületi szögek tételének megfordítása szerint a KM és KO szakaszok hossza ekkor egyenlő. Ez a két szakasz a háromszög csúcsaiból ugyanolyan szög alatt látszik. Vizsgáljuk meg tehát, hogy mi azon P pontok mértani helye, melyekből a két egyenlő szakasz ugyanolyan szög alatt látszik.

 
 

1. ábra
 

Ha egy adott P-re ez a szög φ, akkor P illeszkedik valamelyik, a KM szakaszra emelt φ szöghöz tartozó i látókörívre, és ugyanígy valamelyik, a KO szakaszra emelt φ szögű j látókörívre is. Azt mondjuk, hogy az i ívet a KM szakaszra befelé emeltük, ha az i ív és az O pont a KM egyenesnek ugyanazon az oldalán helyezkednek el; ellenkező esetben kifelé emelt látókörívről beszélünk. Félreértésről itt nem lehet szó, hiszen a feltétel szerint a K, O és M pontok nem esnek egy egyenesre. Ezt a szóhasználatot értelemszerűen követjük a j ívre vonatkozóan is.
Ha az i és j ívet is kifelé emeltük, akkor metszéspontjuk, amennyiben létezik, az MO szakasz f felező merőlegesén helyezkedik el, hiszen KM=KO miatt a két kör egybevágó. Ugyanez a helyzet akkor is, ha mindkét ívet befelé emeltük. Az egyetlen kivétel, ha a két látókörívnek közös K végpontjukon kívül még legalább két közös pontja van. Ez pontosan akkor következik be, ha a két ív ugyanannak a körvonalnak, vagyis a K, O, M pontokra illeszkedő k körvonalnak a része.
Elképzelhető-e, hogy valamelyik ívet (mondjuk az i ívet) kifelé, míg a másik ívet befelé emeltük? A két ív ebben az esetben pontosan akkor metszi egymást, ha φ kisebb a KMO szögnél. Ekkor j metszi az OM szakasz M-en túli meghosszabbítását, ahonnan a KM és KO szakaszok ugyanolyan szög alatt látszanak, vagyis éppen ez a pont lesz a két körív metszéspontja. Egy ilyen pont azonban nem lehet az ABC háromszög csúcsa, mert ekkor az ezen a csúcson és K-n átmenő egyenes nem választaná el az M és O pontok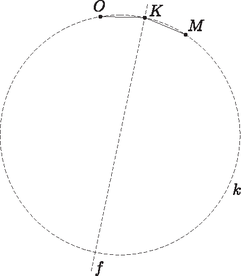at.
 
 

2. ábra
 

Összefoglalva megállapíthatjuk, hogy a háromszög minden egyes csúcsa vagy az f egyenesen, vagy a k körvonalon helyezkedik el. Mivel a K pont illeszkedik f-re, a csúcsok közül legfeljebb egy eshet f-re, vagyis legalább kettő a k körvonalra esik, és éppen ezt kellett bizonyítanunk.
 
II. megoldás (Rácz Béla András megoldása alapján). Jelölje a háromszög csúcsait A, B, C, és tegyük fel, hogy az A, M, K, O pontok egy k körön helyezkednek el. Jegyezzük meg, hogy ez a k kör egyértelmű, hiszen a négy pont különböző. Ahogyan azt az előző megoldás során láttuk, KM=KO, vagyis K illeszkedik az MO szakasz f felező merőlegesére. Jegyezzük meg, hogy a B, O és M pontok nem esnek egy egyenesre, mert abban az esetben AB=BC lenne.
Tekintsük az MBO szög e szögfelezőjének az MBO háromszög köré írt ℓ körrel alkotott L metszéspontját. A kerületi szögek tételének megfordítása miatt ML=LO, vagyis az L pont illeszkedik az f egyenesre. Amint az előző megoldás első felében kiderült, a K pont is illeszkedik az e egyenesre és az f egyenesre, most pedig látszik, hogy ugyanez az L pontra is igaz. Következésképpen, ha az e és f egyenesek nem esnek egybe, akkor K=L, vagyis a B, O, K és M pontok egyaránt az ℓ körre illeszkednek. Mivel a K, O, M pontok különbözők, szükségképpen k=ℓ, vagyis k átmegy a háromszög B csúcsán is.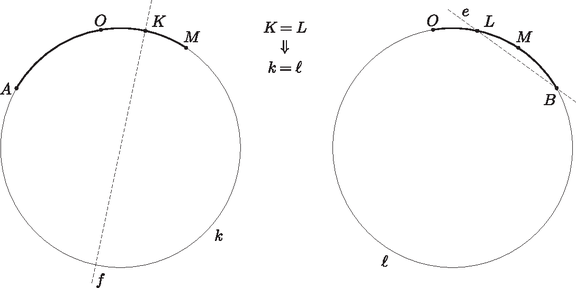
 
 

3. ábra
 

Ha az e és f egyenes egybeesik, akkor f áthalad a B csúcson, vagyis BM=BO=R, ahol R az ABC háromszög köré írt kör sugara. Ha azonban MC az M pontnak az AB oldalra eső merőleges vetülete, akkor 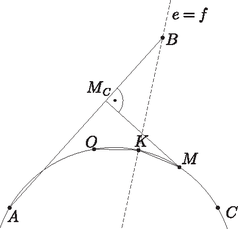BMC=BCcosβ=2Rsinαcosβ, vagyis
BM=BMCsinα=2Rcosβ.
Ezért cosβ=12, β=60∘. Egyszerű szögszámolással adódik, hogy ekkor az AC szakasz az M, K és O pontok mindegyikéből 120∘ szög alatt látszik. Mivel az M, K, O pontok az AC egyenesnek ugyanazon az oldalán vannak, ilyenkor az A, M, K, O, C pontok vannak egy körön, amely nem lehet más, mint k.
 
 

4. ábra

 
III. megoldás (Harangi Viktor megoldása alapján). Ahogyan azt már korábban is láttuk, a K, O, M pontok különbözők, KM=KO és az OM egyenes nem halad át az ABC háromszög egyetlen csúcsán sem. Tegyük fel, hogy az OM egyenes elválasztja az A csúcsot a többi kettőtől. Ekkor az OM szakasz f felező merőlegese (amely illeszkedik a K pontra) szükségképpen metszi a BC oldalt. Ellenkező esetben ugyanis az M és O pontok közül valamelyik (mondjuk M) a B és C pontokhoz is a másiknál közelebb helyezkedne el. Mivel K egyaránt rajta van az MBO és MCO szögek szögfelezőjén, a szögfelező tétel miatt a BK és a CK egyenes is M-hez közelebb metszené az OM szakaszt, ami miatt K is közelebb helyezkedne el M-hez, mint O, ami ellentmondásra vezetne.
A B és C csúcsok közül tehát az egyik az f egyenesnek ugyanazon az oldalán van, mint M, a másik pedig O-val van megegyező oldalon. Az általánosság megszorítása nélkül feltehetjük, hogy BM≤BO és CM≥CO, ahol legalább az egyik helyen határozott egyenlőtlenség áll. Az MO szakaszt tehát a BK egyenes M-hez, a CK egyenes pedig O-hoz metszi közelebb (valamelyik metszéspont esetleg egybeeshet az MO szakasz felezőpontjával, mindkettő azonban nem). Következésképpen az OM egyenes elválasztja a K pontot a B és C csúcsoktól. Megállapíthatjuk tehát, hogy a B és C csúcs is az MKO szögtartományban helyezkedik el.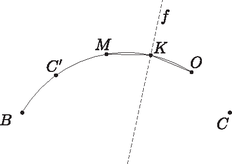
 
 

5. ábra
 

Tükrözzük most a C pontot az f egyenesre, így kapjuk a C' pontot. Ekkor KC'O∢=KCM∢=KCO∢ miatt, és mert C, C' a KO egyenes ugyanazon oldalára esik, láthatjuk, hogy a K, C, C', O pontok egy körön helyezkednek el, ami szimmetria okok miatt az M ponton is átmegy. C tehát illeszkedik a KOM háromszög köré írt körre. Ugyanilyen okok miatt B is illeszkedik erre a körre, az A csúcs viszont nem, hiszen az MO egyenes nem választja el az A és K pontokat. Ezzel az állítást bebizonyítottuk.
 

Megjegyzések. Szükség van-e arra a feltételre, hogy a háromszög oldalai páronként különbözők? Ha a háromszög egyenlő szárú, akkor a K, O, M pontok egy egyenesre esnek. Egy kör tehát csak akkor mehet át mindhárom ponton, ha közülük kettő egybeesik, vagyis ha a háromszög szabályos. Elegendő lett volna tehát annyit feltenni, hogy egy szabályostól különböző hegyesszögű háromszögről van szó.
Ha a háromszög nem hegyesszögű, akkor persze szabályos sem lehet, tehát nincsen szükség ilyen feltételre. Ha azonban a háromszög derékszögű, akkor az M pont egybeesik a háromszög egyik csúcsával. Ha tehát egy kör átmegy a K, O, M pontokon, akkor szükségképpen átmegy a háromszög egyik csúcsán is. Egy másik csúcson viszont akkor és csak akkor mehet át, ha a harmadik csúcsnál lévő szög 60∘. (Miért?) Derékszögű háromszögekre ezek szerint nem érvényes az állítás. Mi a helyzet, ha valamelyik szög tompaszög? Ebben az esetben valamivel több diszkusszióra van szükségünk a megoldás során, az állítás mindazonáltal érvényben marad.
 
Feladatok
1) Egy tompaszögű háromszög magasságpontja M, beírt körének középpontja K, körülírt körének középpontja pedig O. Bizonyítsuk be, hogy ha egy kör átmegy a K, O, M pontokon és a háromszög egyik csúcsán, akkor átmegy egy másik csúcson is.
2) Egy derékszögűtől különböző háromszöghöz pontosan akkor van olyan kör, amely átmegy a K, O, M pontokon és a háromszög egyik csúcsán, ha a háromszög valamelyik szöge 60∘.