Feladat:	A.298	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bóka Gergely ,  Csóka Endre ,  Kunszenti-Kovács Dávid ,  Paulin Roland ,  Rácz Béla András
Füzet:	2003/január, 38 - 41. oldal		PDF  |  MathML
Témakör(ök):	Gömbi geometria, Térgeometriai számítások trigonometriával, Nehéz feladat
Hivatkozás(ok):	Feladatok: 2002/szeptember: A.298

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $O$ a gömb középpontja, amelyen a háromszög elhelyezkedik; a csúcsokat a szokásos módon jelöljük $A$, $B$, $C$-vel. Ha a gömböt és a gömbháromszöget egységnyi sugarúra kicsinyítjük, (1) mindkét oldala a hasonlóság arányának megfelelően változik; ezért az állítást elég egységnyi sugarú gömbre igazolni. Továbbá, ha $\alpha$ és $\beta$ egyike sem hegyesszög, az állítás triviális, mert $\text{cos}\alpha$ és $\text{cos}\beta$ nempozitív. Ezért, figyelembe véve, hogy az állítás az $\alpha$ és $\beta$ felcserélésére szimmetrikus, azt is feltételezhetjük, hogy $\alpha$ hegyesszög. Tekintsük az $OAB$, $OBC$ és $OAC$ körcikkeket; ezek területe $\frac{c}{2}$, $\frac{a}{2}$, illetve $\frac{b}{2}$. Vetítsük az $OBC$ és $OAC$ körcikkeket az $OAB$ síkra. Egy síkbeli alakzat merőleges vetítésekor a vetület és az eredeti alakzat területének aránya a két sík bezárt szögének koszinusza, tehát a körcikkek vetületének területe $\frac{a}{2}|\text{cos}\beta |$, illetve $\frac{b}{2}\text{cos}\alpha$. A továbbiakban három esetet fogunk megkülönböztetni attól függően, hogy $\beta$ hegyes-, tompa- vagy derékszög. 1. eset: $\beta$ hegyesszög. Ebben az esetben a $C\text{'}$ pont az $OAB$ körcikk belsejébe esik (1. ábra). Az $AC$ és $BC$ körívek vetületei egy $AA\text{'}$, illetve $BB\text{'}$ nagytengelyű ellipszis megfelelő ívei. A két ellipszis az $OAB$, $OBA\text{'}$, $OA\text{'}B\text{'}$ és $OB\text{'}A$ körcikkek mindegyikében metszi egymást. Mindegyik tartományban csak egy-egy metszéspontjuk van, mert két kúpszeletnek legfeljebb négy közös pontja lehet. 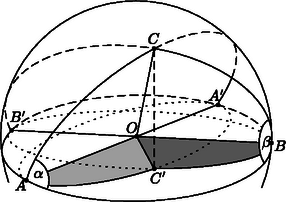    1. ábra   Az $OBC$ és $OAC$ körcikkek vetületei részei az $OAB$ körcikknek, azt nem fedik le teljesen és nem nyúlnak egymásba. Ezért területük összege kisebb, mint az $OAB$ körcikk területe: $\frac{a}{2}\text{cos}\beta +\frac{b}{2}\text{cos}\alpha <\frac{c}{2}$. Ez éppen a bizonyítandó állítás. 2. eset: $\beta$ derékszög. Ekkor a $C\text{'}$ pont az $OB$ szakasz belsejébe esik (2. ábra). Az $OAC$ körcikk vetülete valódi része az $OAB$ körcikknek, a területe tehát kisebb: $\frac{b}{2}\text{cos}\alpha <\frac{c}{2}$. Mivel $\text{cos}\beta =0$, ez éppen az állítás. 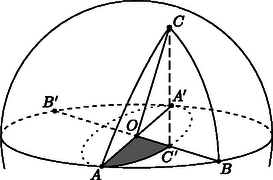    2. ábra   3. eset: $\beta$ tompaszög. Ekkor a $C\text{'}$ pont az $OBA\text{'}$ körcikk belsejébe esik (3. ábra). Mivel $\text{cos}\beta$ negatív, (1) baloldalán az $OAC$ és $OBC$ körcikkek vetületeinek, azaz az $OAC\text{'}$ és $OBC\text{'}$ ellipszisdarabok területének különbsége áll. Az $OAC\text{'}$ ellipszisdarab kilóg az $OAB$ körcikkből, de a kilógó részt az $OBC\text{'}$ ellipszisdarab teljesen lefedi. Ezért a két ellipszisdarab területének különbsége kisebb, mint az $OAB$ körcikk területe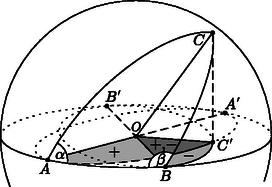: $\frac{b}{2}\text{cos}\alpha -\frac{a}{2}|\text{cos}\beta |<\frac{c}{2}$, azaz $b\text{cos}\alpha +a\text{cos}\beta <c$.     3. ábra   () Bóka Gergely, Csóka Endre és Paulin Roland dolgozata alapján   Megjegyzés. A megoldásból jól látható, hogy a gömbháromszög vetületének területe az $OAB$ síkon minden esetben $\frac{c}{2}-\frac{a}{2}\text{cos}\beta -\frac{b}{2}\text{cos}\alpha$.   II. megoldás. Ismét feltételezzük, hogy a gömb sugara egységnyi. Az $a$, $b$ és $c$ ívhosszakra teljesül a háromszög-egyenlőtlenség, ezért ilyen hosszúságú szakaszokból a síkban is háromszög szerkeszthető. Legyenek a síkbeli $a$, $b$, $c$ oldalú háromszög megfelelő szögei rendre $\alpha \text{'}$, $\beta \text{'}$ és $\gamma \text{'}$. A síkban $a\cdot \text{cos}\beta \text{'}+b\cdot \text{cos}\alpha \text{'}=c$, mert $a\cdot \text{cos}\beta \text{'}$ és $b\cdot \text{cos}\alpha \text{'}$ nem más, mint az $a$ és $b$ oldalak vetületének előjeles hossza a $c$ oldalon. Az összefüggés hegyes-, derék- és tompaszögű háromszögekben egyaránt érvényes (4. ábra). Ezért elég azt igazolnunk, hogy 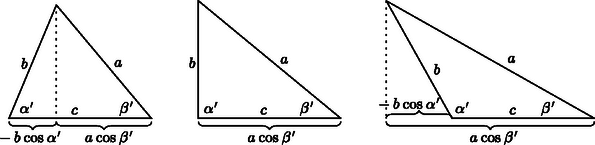    4. ábra   $\text{cos}\alpha <\text{cos}\alpha \text{'}$ és $\text{cos}\beta <\text{cos}\beta \text{'}$, azaz $\alpha >\alpha \text{'}$ és $\beta >\beta \text{'}$. A két egyenlőtlenség csupán az $a$ és $b$ oldalak szerepének felcserélésében különbözik, ezért elég az előbbit bizonyítani. A bizonyításhoz felhasználjuk a gömbi koszinusztételt, valamint azt az ismert tényt, hogy a gömbháromszög kerülete kisebb, mint $2\pi$. (Ezeket a kedves Olvasó megtalálhatja például Reiman István A geometria és határterületei c. könyvében.) A koszinusztételből $1+\text{cos}\alpha \text{'}=\frac{b^2+c^2-a^2+2bc}{2bc}=\frac{\left(b+c+a\right)\left(b+c-a\right)}{2bc}$. A szögekre vonatkozó gömbi koszinusztétel szerint $\begin{array}{c}{\displaystyle \text{cos}a=\text{cos}b\text{cos}c+\text{sin}b\text{sin}c\text{cos}\alpha \mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle 1+\text{cos}\alpha }& \hfill {\displaystyle =}\hfill & {\displaystyle \frac{\text{cos}a-\text{cos}b\text{cos}c+\text{sin}b\text{sin}c}{\text{sin}b\text{sin}c}=}\hfill \\ \hfill {\displaystyle }& \hfill {\displaystyle =}\hfill & {\displaystyle \frac{\text{cos}a-\text{cos}\left(b+c\right)}{\text{sin}b\text{sin}c}=\frac{2\text{sin}\frac{b+c+a}{2}\text{sin}\frac{b+c-a}{2}}{\text{sin}b\text{sin}c}\mathrm{.}}\hfill \end{array}}}\end{array}$ A bizonyítandó állítás tehát: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{2\text{sin}\frac{b+c+a}{2}\text{sin}\frac{b+c-a}{2}}{\text{sin}b\text{sin}c}}& \hfill {\displaystyle <}\hfill & {\displaystyle \frac{\left(b+c+a\right)\left(b+c-a\right)}{2bc}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 12pt"> </div>}}\\ \hfill {\displaystyle \frac{\text{sin}\frac{b+c+a}{2}}{\frac{b+c+a}{2}}\cdot \frac{\text{sin}\frac{b+c-a}{2}}{\frac{b+c-a}{2}}}& \hfill {\displaystyle <}\hfill & {\displaystyle \frac{\text{sin}b}{b}\cdot \frac{\text{sin}c}{c}\mathrm{.}}\hfill \end{array}}}\end{array}$ Legyen $p=\frac{b+c-a}{2}$ és $q=\frac{b+c+a}{2}$. A háromszög-egyenlőtlenségből, valamint az $a+b+c<2\pi$ egyenlőtlenségből következik, hogy $0<p<b\mathrm{,}c<q<\pi$, továbbá a definícióból $p+q=b+c$. Legyen $f\left(t\right)=\text{ln}\frac{\text{sin}t}{t}$; azt kell igazolnunk, hogy $f\left(p\right)+f\left(q\right)<f\left(b\right)+f\left(c\right)$. Vizsgáljuk meg az $f$ függvényt a $\left(\mathrm{0,}\pi \right)$ intervallumban. A függvény második deriváltja negatív: $\begin{array}{c}{\displaystyle f\text{'}\text{'}\left(t\right)=\left(\text{ctg}t-\frac{1}{t}\right)\text{'}=\frac{1}{t^2}-\frac{1}{\text{sin}{}^{2}t}<\mathrm{0,}}\end{array}$ tehát a függvény szigorúan konkáv. Ebből következik, hogy $\begin{array}{c}{\displaystyle f\left(b\right)+f\left(c\right)>\left(\frac{q-b}{q-p}f\left(p\right)+\frac{b-p}{q-p}f\left(q\right)\right)+\left(\frac{q-c}{q-p}f\left(p\right)+\frac{c-p}{q-p}f\left(q\right)\right)=f\left(p\right)+f\left(q\right)\mathrm{.}}\end{array}$ () Rácz Béla András dolgozata alapján