Kezdőlap


Feladat:	B.3524	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Pálinkás Csaba , Szilágyi Péter
Füzet:	2002/november, 485 - 487. oldal		PDF \| MathML
Témakör(ök):	Negyed- és magasabb fokú függvények, Függvényvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 2002/február: B.3524

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A vizsgált kifejezés szimmetrikus, így felírható $x + y (= 1)$ és $x y = t$ polinomjaként. Valóban:

\begin{matrix} A (x, y) = x y^{4} + x^{4} y = x y (x^{3} + y^{3}) = x y [(x + y) (x^{2} - x y + y^{2})] . \end{matrix}

Mivel

x^{2} - x y + y^{2} = {(x + y)}^{2} - 3 x y

, azért

\begin{matrix} A (x, y) = x y [(x + y) ({(x + y)}^{2} - 3 x y)] = x y (1 - 3 x y) . \end{matrix}

x + y

=1, akkor az

x y = t

szorzat értékkészlete a

] - \infty; 1 / 4]

intervallum, ugyanis az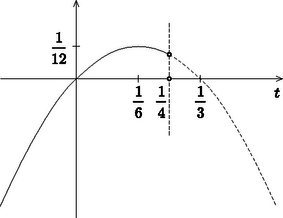

\begin{matrix} \begin{matrix} x + y & = & 1 \\ x y & = & t \end{matrix}} \end{matrix}

egyenletrendszerből kapott másodfokú egyenlet diszkriminánsa

D = 1 - 4 t

, az egyenletrendszernek akkor és csak akkor van valós megoldása, ha

t \leq \frac{1}{4}

1. ábra

x + y = 1

feltétel esetén tehát a kétváltozós

A (x, y)

polinom értékkészlete az

I =] - \infty; 1 / 4]

intervallumon megegyezik az

f (t) = t (1 - 3 t)

függvény értékkészletével (1. ábra). A valós számok halmazára kiterjesztett

f

függvény a

t = \frac{1}{6}

helyen veszi föl az abszolút maximumát és ez az érték

f (\frac{1}{6}) = \frac{1}{12}

. Mivel

\frac{1}{6} \in I

, azért ennyi az

I

intervallumon értelmezett

f (t)

függvény maximuma, tehát a szóban forgó

A (x, y)

legnagyobb értéke is az

x + y = 1

feltétel esetén.

Pálinkás Csaba (Szolnok, Verseghy F. Gimn. 9. évf.)

Megjegyzések. 1. A megoldók többsége az

x y^{4} + x^{4} y

kifejezést az

x + y

=1 feltételt felhasználva

- 3 {(x y - \frac{1}{6})}^{2} + \frac{1}{12}

alakba írta. Több mint 100 dolgozatban ezek után minden további nélkül olyasmi szerepelt, hogy eszerint a keresett maximum értéke

\frac{1}{12}

. Ez csak akkor igaz, ha az összeg első tagja,

- 3 {(x y - \frac{1}{6})}^{2}

fölveszi a 0 értéket, azaz van olyan

x

és

y

, melyek összege 1, szorzatuk pedig

\frac{1}{6}

. A megoldásból ez kiderül, bár ott ezeket az értékeket nem számoltuk ki. Az

\begin{matrix} \begin{matrix} x + y & = & 1 \\ x y & = & \frac{1}{6} \end{matrix}} \end{matrix}

egyenletrendszer megoldásával nyomban adódnak a változóknak azok az értékei, amelyekre

A (x, y)

maximális:

{x, y} = {\frac{3 - \sqrt[]{3}}{6}, \frac{3 + \sqrt[]{3}}{6}} .

2. A feladat eredménye szerint ha

x + y

=1, akkor

x y^{4} + x^{4} y \leq \frac{1}{6}

. Ebben a formában arra a ritkább jelenségre láthatunk példát, amikor egy szimmetrikus egyenlőtlenségben nem a változók egyenlő értékeire kapjuk a maximumot.
II. megoldás. A feladatot a differenciálszámítás alkalmazásával oldjuk meg. Az eredetileg kétváltozós függvényt az

y = 1 - x

helyettesítéssel egyváltozós polinommá írhatjuk:

\begin{matrix} f (x) = x {(1 - x)}^{4} + x^{4} (1 - x) . \end{matrix}

Írjuk föl a függvény deriváltját, majd a hatványozás elvégzése után rendezzük a polinomot:

\begin{matrix} f' (x) = {(1 - x)}^{4} - 4 x {(1 - x)}^{3} + 4 x^{3} (1 - x) - x^{4} = - 12 x^{3} + 18 x^{2} - 8 x + 1. \end{matrix}

Az eredeti kétváltozós polinom szimmetrikus, így teljesül, hogy

f (x) = f (1 - x)

. A deriváltra nézve innen

f' (x) = - f' (1 - x)

adódik, azaz

f' (\frac{1}{2}) = - f' (\frac{1}{2})

és így

f' (\frac{1}{2}) = 0

következik. Ennek alapján a derivált szorzattá alakítható:

\begin{matrix} f' (x) = (x - \frac{1}{2}) (- 12 x^{2} + 12 x - 2) . \end{matrix}

A másodfokú tényezőnek két valós gyöke van,

x_{1} = \frac{3 - \sqrt[]{3}}{6}

és

x_{2} = \frac{3 + \sqrt[]{3}}{6}

. Jegyezzük meg, hogy

x_{1} + x_{2} = 1

miatt

f (x_{1}) = f (x_{2})

.
Mivel a harmadfokú

f' (x)

-nek három különböző valós gyöke van és a főegyütthatója negatív, a grafikonja fölvázolható: (2. ábra). A grafikonról leolvasható a derivált előjele, és így az is, hogy

f

-nek két lokális maximuma van:

x_{1}

-ben és

x_{2}

-ben. Azt már láttuk, hogy ezek a maximumok egyenlők és mivel

f

szigorúan monoton növő, ha

x < x_{1}

és szigorúan monoton fogyó, ha

x > x_{2}

, azért ez a közös érték,

f (x_{1}) = f (x_{2}) = \frac{1}{12}

a függvény abszolút maximuma.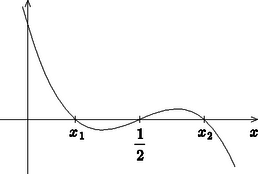

2. ábra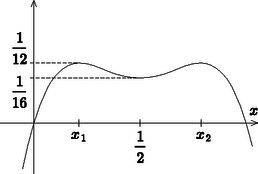

3. ábra

Szilágyi Péter (Debrecen, Kossuth L. Gyak. Gimn. 10. évf.)

Megjegyzés. A fenti vizsgálatból az is kiderül, hogy

f

-nek lokális minimuma van, ha

x = \frac{1}{2}

; ennek értéke

f (\frac{1}{2}) = \frac{1}{16}

. Az

f

függvény grafikonja a 3. ábrán látható.