Kezdőlap


Feladat:	B.3510	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bóka Gergely , Dúró Dóra , Gyarmati Ákos , Koltai Péter , Kovács Dóra Judit , Kovács Levente , Pálinkás Csaba , Pásztor Péter , Rácz Béla András , Salát Máté , Seres Gyula , Slíz György , Ta Vinh Thong , Takács Gergő , Tancsa Balázs , Zsbán Ambrus
Füzet:	2002/október, 411. oldal		PDF \| MathML
Témakör(ök):	Térgeometriai bizonyítások, Tetraéderek, Vektorok lineáris kombinációi, Feladat
Hivatkozás(ok):	Feladatok: 2001/december: B.3510

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C D$ tetraéder súlypontja $S$ , $\vec{S A} = a$ , $\vec{S B} = b$ , $\vec{S C} = c$ és $\vec{S D} = d$ . Mivel $S$ súlypont, azért

\begin{matrix} a + b + c + d = 0 . \end{matrix}

(1)

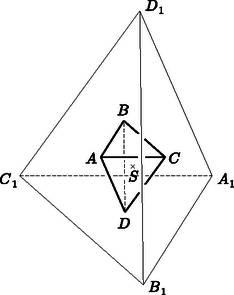Alkalmazzunk az

A B C D

tetraéderre

S

középpontú,

- 3

arányú középpontos hasonlóságot, legyen ennek során a tetraéder képe az

A_{1} B_{1} C_{1} D_{1}

tetraéder. A hasonlóságnál sík és képe párhuzamosak, ezért az

A_{1} B_{1} C_{1} D_{1}

tetraéder lapsíkjai párhuzamosak az

A B C D

tetraéder lapsíkjaival. A hasonlóság aránya

- 3

, ezért

a_{1} = \vec{S A_{1}} = - 3 a

b_{1} = \vec{S B_{1}} = - 3 b

c_{1} = \vec{S C_{1}} = - 3 c

és

d_{1} = \vec{S D_{1}} = - 3 d

. Legyen az

A_{1} B_{1} C_{1}

háromszög súlypontja

S_{D}

. Ekkor a súlypontra vonatkozó ismert összefüggést és (1)-et felhasználva:

\begin{matrix} \vec{S S_{D}} = \frac{a_{1} + b_{1} + c_{1}}{3} = - a - b - c = d . \end{matrix}

Ez azt jelenti, hogy az

A_{1} B_{1} C_{1}

háromszög súlypontja

D

. Így

D

rajta van az

A_{1} B_{1} C_{1}

síkon, és mivel egy ponton át egy adott síkkal pontosan egy párhuzamos sík fektethető, az

A_{1} B_{1} C_{1}

sík éppen a feladatunkban szereplő,

D

-n átmenő,

A B C

síkkal párhuzamos sík.
Ugyanígy látható be, hogy az

A_{1} B_{1} C_{1} D_{1}

tetraéder többi lapsíkja is átmegy az

A B C D

tetraéder megfelelő csúcsain, illetve hogy a további lapok súlypontjai rendre

A

B

és

C

, amivel feladatunk állítását bebizonyítottuk.