Kezdőlap


Feladat:	B.3503	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kovács Levente
Füzet:	2002/október, 409 - 410. oldal		PDF \| MathML
Témakör(ök):	Négyszögek geometriája, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 2001/december: B.3503

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük a négyszög csúcsait az 1. ábrán látható módon $A$ , $B$ , $C$ , $D$ -vel, az $A B$ oldal felezőpontja legyen $E$ , az $C D$ oldalé pedig $F$ . Legyen $C$ -nek a $B F$ szakasz felezőpontjára vonatkozó tükörképe $G$ , $D$ -nek az $A F$ szakasz felezőpontjára vonatkozó tükörképe pedig $H$ . Ekkor a $B C F G$ és az $A D F H$ négyszögek paralelogrammák. Ezért $B G$ párhuzamos és egyenlő $C F$ -fel, $A H$ pedig párhuzamos és egyenlő $D F$ -fel. Viszont $F$ a $C D$ szakasz felezőpontja, tehát $B G$ párhuzamos és egyenlő $A H$ -val, azaz a $B G A H$ négyszög is paralelogramma. Ezért $A B$ átlójának $E$ felezőpontja a $G H$ átlóját is felezi. Ezek szerint a $G H F$ háromszögben $F E$ súlyvonal.

1. ábra

G H F

háromszögben az

F E = f

súlyvonalon kívül két oldalt is ismerünk, mert

G F = B C = b

és

H F = A D = d

. Ezekből az adatokból a

G H F

háromszög egyszerűen megszerkeszthető: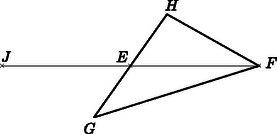

2. ábra

Vegyük fel az

F J = 2 f

szakaszt, jelöljük ki ennek

E

felezőpontját, majd szerkesszük meg a

J

középpontú,

d

sugarú és az

F

középpontú,

b

sugarú körök

G

metszéspontját (2. ábra). Tükrözzük végül

G

-t

E

-re, a tükörkép legyen

H

. Az így szerkesztett

G H F

háromszögben

F E = f

nyilván súlyvonal,

F G = b

, továbbá

H F

éppen

G J

E

-re vonatkozó tükörképe, tehát

H F = d

.
Az

E

és

H

pontok ismeretében

A

-t az

E

középpontú,

\frac{a}{2}

sugarú és a

H

középpontú,

\frac{c}{2} (= F D)

sugarú körök metszéspontjaként kapjuk.

A

-t

E

-re tükrözve kapjuk

B

-t, végül

G

-t

B F

H

-t pedig

A F

felezőpontjára tükrözve kapjuk a négyszög

C

és

D

csúcsait.
Szerkesztésünkből következik, hogy az

A B C D

négyszög megfelel a feltételeknek, mert

A B = 2 \cdot A E = 2 \cdot \frac{a}{2} = a

B C = F G = b

A D = H F = d

D F

egyenlő

F C

-vel, hosszuk egyenként

\frac{c}{2}

, tehát

F

és

E

oldalfelezőpontok és

F E = f

.
Feltételként szerepelt, hogy a feladatnak van megoldása, azért

b + d \geq 2 f

. Ha

b + d > 2 f

, akkor a

G H F

háromszög, s így az

A B C D

négyszög is lényegében egyértelműen szerkeszthető meg. Ha

b + d = 2 f

, akkor

b \neq d

esetén ugyancsak egyértelmű a szerkesztés (bár a

G H F

háromszög elfajuló), ha viszont

b = d = f

, akkor végtelen sok megoldás van, ekkor ugyanis az

A B C D

négyszög paralelogramma (3. ábra).

3. ábra

Kovács Levente (Budapest, Szent István Gimn., 10. évf.) dolgozata alapján