Kezdőlap


Feladat:	B.3498	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2002/szeptember, 337 - 338. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Derékszögű háromszögek geometriája, Beírt kör, Szögfelező egyenes, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 2001/november: B.3498

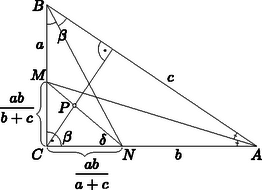
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Feltehetjük, hogy $M$ a $B C$ , $N$ pedig az $A C$ oldalon van. Jelöljük a háromszög oldalait a szokásos módon $a$ , $b$ , $c$ -vel, a $B$ -nél lévő szögét $β$ -val. Legyen továbbá $P N C ∢ = δ$ (lásd az ábrát).

A szögfelezőtétel szerint

\frac{C M}{M B} = \frac{b}{c}

, ezért

C M = \frac{b}{b + c} \cdot C B = \frac{a \cdot b}{b + c}

. Ugyanígy kapjuk, hogy

\begin{matrix} C N = \frac{a \cdot b}{a + c} . \end{matrix}

(1)

Mivel a

C P

egyenes merőleges

A B

-re, azért a

P C N ∢

és az

A B C ∢

merőleges szárú hegyesszögek, tehát

P C N ∢ = β

. A

P C N

háromszög

P

-nél lévő szöge így

180^{\circ} - β - δ

. Ebben a háromszögben a szinusztétel szerint

\begin{matrix} \frac{C N}{C P} & = & \frac{sin (180^{\circ} - β - δ)}{sin δ} = \frac{sin (β + δ)}{sin δ} = \\ = & \frac{sin β cos δ + cos β sin δ}{sin δ} = sin β \cdot ctg δ + cos β . \end{matrix}

A szögfüggvények értékeit az

A B C

, illetve az

N M C

háromszög oldalaival kifejezve kapjuk, hogy

\begin{matrix} \frac{C N}{C P} = \frac{b}{c} \cdot (\frac{a \cdot b}{a + c} / \frac{a \cdot b}{b + c}) + \frac{a}{c} = \frac{b \cdot (b + c)}{c \cdot (a + c)} + \frac{a}{c} = \frac{a^{2} + b^{2} + c \cdot (a + b)}{c \cdot (a + c)} . \end{matrix}

Felhasználva Pitagorasz tételét, valamint az (1) összefüggést, ebből

\begin{matrix} C P = C N \cdot \frac{c (a + c)}{c^{2} + c (a + b)} = \frac{a \cdot b}{a + b + c} \end{matrix}

(2)

adódik.
Ismert, hogy ha egy háromszög területe

T

, beírt körének sugara

r

, oldalai pedig

a

b

c

, akkor

r = \frac{2 T}{a + b + c}

. Mivel esetünkben az

A B C

derékszögű háromszög befogói

a

és

b

, azért

2 T = a \cdot b

, tehát a (2) összefüggésből következik, hogy

C P = r

, ami éppen a bizonyítandó állítás.