Feladat: B.3480 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balogh János ,  Herczeg Attila ,  Horváth Márton ,  Kiss-Tóth Christián ,  Kocsis Albert Tihamér ,  Maga Péter ,  Pallos Péter ,  Pongrácz András ,  Rácz Béla András ,  Rácz Éva ,  Sparing Dániel ,  Tóth János 
Füzet: 2002/április, 215 - 218. oldal  PDF  |  MathML 
Témakör(ök): Inverzió, Tengelyes tükrözés, Középpontos és egyéb hasonlósági transzformációk, Kör (és részhalmaza), mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 2001/szeptember: B.3480

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az e egyenes pontjait tekintve az AB és a CD zárt intervallumok egyesítésén kívüli pontokra APB∢=CPD∢=0∘, az egyenes további pontjaiból pedig az egyik szakasz 0∘,a másik pedig 180∘-os szögben látszik, illetve ha P egybeesik valamelyik megadott ponttal, akkor az egyik szög nem értelmezhető. Az e egyenesen tehát az AB és CD zárt szakaszok kivételével minden pont megfelelő (1. ábra).

 

 
1. ábra
 

Legyen most P∉e és tegyük föl, hogy APB∢=CPD∢. A keresett ponthalmaz szimmetrikus az e egyenesre, így elegendő az e által határolt egyik félsíkban vizsgálni a keresett pontokat.
Vizsgáljuk először a ,,szimmetrikus'' esetet, amikor a két szakasz egyenlő, AB=CD. Az az eltolás, ami az AB szakaszt a CD-be viszi, az A, B, P pontokon átmenő k kört ‐ ez most létrejön ‐ a C, D pontokon átmenő k' körbe viszi (2. ábra). Ha P képe P', akkor nyilván APB∢=CP'D∢, ez utóbbi tehát a feltétel szerint egyenlő a CPD∢ szöggel. Mivel P és P' ugyanabban a félsíkban vannak, azért a látókör mértani hely tulajdonsága miatt P is rajta van a k' körön, a P pont tehát a k és k' körök ‐ egyik ‐ közös pontja.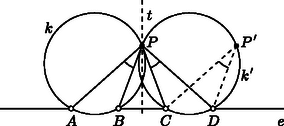
 

 
2. ábra
 

A k' kört viszont a k tükörképeként is megkapjuk, ha a tükrözés tengelye az AB és CD szakaszok t szimmetriatengelye. Mivel pedig körnek és tükörképének a közös pontjai ‐ ha vannak ‐ illeszkednek a tükrözés tengelyére, a P pont rajta van a t egyenesen. Az pedig nyilvánvaló, hogy ennek a tengelynek minden pontja hozzátartozik a keresett halmazhoz.
A fenti gondolatmenet alkalmas kiterjesztésével az általános, AB≠CD esetben is megkapjuk a megoldást. Tekintsük azt a pozitív arányú középpontos hasonlóságot, ami az AB szakaszt a CD-be viszi. (Ha AB≠CD, akkor ilyen létezik, középpontja, O, az e egyenesen van, aránya λ=CDAB). Az A, B, P pontokon átmenő k kört ez a hasonlóság a C, D pontokon átmenő k' körbe viszi (3. ábra).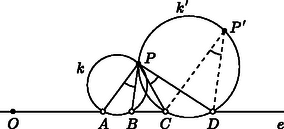
 

 
3. ábra
 

Ha P képe P', akkor a speciális eset gondolatmenetét követve APB∢=CP'D∢, hiszen a középpontos hasonlóság szögtartó, a feltétel szerint pedig APB∢=CPD∢. Így CP'D∢=CPD∢, P a k' körön is rajta van, a két kör, k és k' a P pontban metszik egymást.
Az O pont választásából 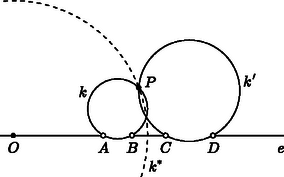OAOB=OCOD, azaz
OA⋅OD=OC⋅OB,
az AB szakaszt tehát a középpontos hasonlóságon kívül az O pólusú,
r=OA⋅OD=OC⋅OB
sugarú inverzió is a CD szakaszba viszi (4. ábra). Ez az inverzió a k kört egy olyan körbe viszi, ami átmegy a C és D pontokon, továbbá az inverzió pólusa, O hasonlósági centruma a k körnek és a képének. Mindez egyértelműen határozza meg a k' kört, így a k kört a fenti inverzió is a k'-be viszi. Ha pedig egy kör és az inverze metszik egymást, akkor a metszéspont rajta van az inverzió alapkörén. A P pont így rajta van az O középpontú r sugarú k* körön.
 

 
4. ábra
 

Megmutatjuk, hogy k* minden pontja hozzátartozik a keresett ponthalmazhoz.
A k* elválasztja az AB és a CD szakaszokat, így az a két pont, ahol az e egyenest metszi, a mértani helyhez tartozik. Ha P olyan pont a k* körön, ami nincs rajta az e egyenesen, akkor az A, B, P pontokon átmenő k kört mind az O középpontú λ=CDAB arányú hasonlóság, mind pedig a k* körre vonatkozó inverzió ugyanabba a k' körbe viszi (5. ábra). Mivel az inverzió során a P képe önmaga, a P ponton a k' kör is áthalad. Ha pedig a középpontos hasonlóság során a P képe P', akkor a APB∢=CP'D∢, a kerületi szögek tétele szerint pedig a k' körben CP'D∢=CPD∢. A két egyenlőséget összevetve 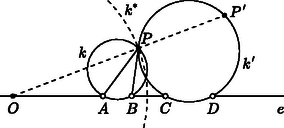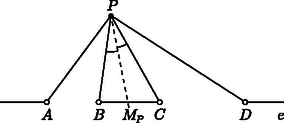APB∢=CPD∢ valóban.
 

 
5. ábra
 

 
II. megoldás. Húzzuk meg a BPC szög belső szögfelezőjét és messe ez az e egyenest a P-től függő MP pontban. Nyilvánvaló, hogy APB∢=CPD∢ pontosan akkor teljesül, ha PMP felezi az APD∢ szöget is (6. ábra). Ha AP=PD, akkor PMP merőleges az e-re és így BP=PC is teljesül, MP felezi AD-t és BC-t is, tehát AB=CD, az ábra szimmetrikus a PMP egyenesre, P tehát rajta van a szimmetriatengelyen, amelynek nyilván minden pontja megfelelő.
 

 
6. ábra
 

A továbbiakban tegyük fel, hogy AB≠CD, ami azt jelenti, hogy az APPD=λ1, illetve a BPPC=λ2 arányok értéke nem 1. Ez azt jelenti, hogy P rajta van az A és D pontokhoz tartozó λ1, illetve a B és C pontokhoz tartozó λ2 arányú Apollóniusz-féle körön. A szögfelező-tétel szerint mindkét kör áthalad az MP ponton is, így a körök középpontja rajta van PMP felező merőlegesén, ami most nem párhuzamos e-vel. Ismeretes, hogy a körök középpontja az e egyenesen is rajta van, ez viszont azt jelenti, hogy a két Apollóniusz-kör középpontja egybeesik, a két kör tehát azonos (7. ábra).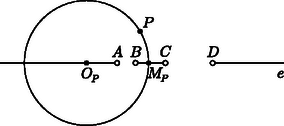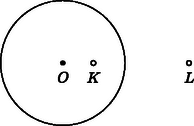
 

 
7. ábra
 

 

 
8. ábra
 

Jelölje a körök közös középpontját OP. Ismeretes, hogy ha a K, L pontokhoz tartozó λ≠1 arányú Apollóniusz-kör középpontja O, sugara r, akkor OK⋅OL=r2 (8. ábra). A két kör középpontja és sugara most azonos, így
r2=OPA⋅OPD=OPB⋅OPC.
A kapott egyenlőséget átrendezve OPCOPA=OPDOPB, az OP tehát az a pont az e egyenesen, ahonnan az AB szakaszt a CD-be nagyítható (vagy kicsinyíthető). Ennek a pontnak a helyzete pedig nem függ a P ponttól, csak az AB és CD szakaszok helyzetétől, OP=O a két szakasz külső hasonlósági pontja. Az MP=M pont helyzete sem függ tehát P-től és a két egybeeső Apollóniusz-kör sem. Ha tehát AB≠CD és APB∢=CPD∢, akkor P rajta van az O középpontú r=OA⋅OD=OB⋅OC sugarú körön, ahol O a két szakasz, AB és CD külső hasonlósági pontja.
A megfordítás most már nyomban adódik az Apollóniusz-féle kör mértani hely tulajdonságából és a szögfelező-tételből. Ha P egy tetszőleges pont a közös Apollóniusz-körön és P∉e ‐ ami nyilván föltehető ‐ akkor egyrészt APPD=AMMD és így PM felezi az APD∢ szöget, másfelől ugyanígy BPPC=BMMC és így PM felezi a BPC∢ szöget is. Ebből pedig valóban APB∢=CPD∢ következik.