Feladat:	B.3476	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bergmann Gábor
Füzet:	2002/április, 214 - 215. oldal		PDF  |  MathML
Témakör(ök):	Háromszög területe, Síkgeometriai bizonyítások, Szabályos sokszögek geometriája, Vektorok, Vektorok vektoriális szorzata, Feladat
Hivatkozás(ok):	Feladatok: 2001/szeptember: B.3476

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Vizsgáljuk meg egy adott kék háromszög és a vele szemben lévő piros háromszög területének különbségét. Ha a tízszög oldalának hosszát 2 egységnek választjuk, akkor minden színes háromszög területének mérőszáma megegyezik a háromszög azon magasságának mérőszámával, amely a tízszög belsejében kijelölt $P$ ponthoz tartozik. Ezért két szemközti háromszög területének különbsége egyenlő a $P$-ből induló magasságaik különbségével. Mivel a tízszög szemközti oldalai párhuzamosak, azért a két magasságvonal egy egyenesbe esik. Így a két magasságszakasz különbsége megegyezik a $PF$ távolság kétszeresével, ahol $F$ a tízszög két párhuzamos oldala által a magasságok közös egyeneséből kimetszett szakasz felezőpontja (lásd az 1. ábrát). 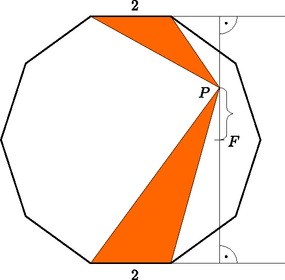    1. ábra   Jelöljük a tízszög középpontját $O$-val, ${\text{m}}_1$, ${\text{m}}_2$, ${\text{m}}_3$, ${\text{m}}_4$ és ${\text{m}}_5$ pedig legyenek olyan $O$-ból induló egységvektorok, amelyek merőlegesek a tízszög egy-egy szemközti oldalpárjára, és az oldalpárnak mindig a piros háromszöghöz tartozó oldala felé mutatnak. Ezen öt vektor összege 0; tekinthetjük őket ugyanis egy szabályos ötszög középpontjából az ötszög csúcsaiba mutató vektoroknak. Mivel $PF$ párhuzamos valamelyik m${}_i$ vektorral, azért az előjeles $PF$ távolság éppen $\overrightarrow{OP}\cdot {\text{m}}_i$ $PF=OP\cdot \text{cos}\alpha =\overrightarrow{OP}\cdot {\text{m}}_1$, (2. ábra). Vagyis a piros és a kék háromszögek területkülönbségének összege: 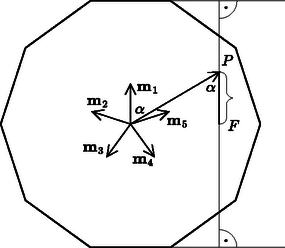$\begin{array}{c}{\displaystyle 2\overrightarrow{OP}\cdot {\text{m}}_1+2\overrightarrow{OP}\cdot {\text{m}}_2+2\overrightarrow{OP}\cdot {\text{m}}_3+2\overrightarrow{OP}\cdot {\text{m}}_4+2\overrightarrow{OP}\cdot {\text{m}}_5=2\overrightarrow{OP}\cdot \text{0}=\mathrm{0,}}\end{array}$ azaz a piros és a kék területek egyenlőek.     2. ábra   Bergmann Gábor (Budapest, Berzsenyi D. Gimn., 11. évf.) II. megoldás. Ismert, hogy ha egy háromszög egyik csúcsából a másik két csúcsba mutató vektorok $\text{x}$ és $\text{y}$, akkor a háromszög területének kétszerese $|\text{x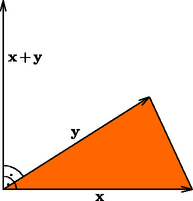}\times \text{y}|$ (3. ábra).     3. ábra   Jelöljük a tízszög középpontjából a sokszög csúcsaiba mutató vektorokat ${\text{a}}_1\mathrm{,}{\text{a}}_2\mathrm{,}\text{...}\mathrm{,}{\text{a}}_{10}$-zel, az adott belső pontba mutató vektort pedig $\text{p}$-vel. A sokszög területe ekkor $5|{\text{a}}_1\times {\text{a}}_2|$, továbbá nyilván igaz, hogy ${\text{a}}_i\times {\text{a}}_{i+1}={\text{a}}_{i+1}\times {\text{a}}_{i+2}$ (az indexeket modulo 10 értve). Elegendő azt megmutatnunk, hogy a kék háromszögek területének kétszerese megegyezik a tízszög területével, azaz $\begin{array}{c}{\displaystyle |\left({\text{a}}_1-\text{p}\right)\times \left({\text{a}}_2-\text{p}\right)+\left({\text{a}}_3-\text{p}\right)\times \left({\text{a}}_4-\text{p}\right)+\text{...}+\left({\text{a}}_9-\text{p}\right)\times \left({\text{a}}_{10}-\text{p}\right)|=5|{\text{a}}_1\times {\text{a}}_2|\mathrm{.}}\end{array}$ Ez viszont azonnal adódik, ha a bal oldalon elvégezzük a műveleteket és felhasználjuk, hogy $\text{p}\times \text{p}=\text{0}$, valamint ${\text{a}}_1+{\text{a}}_2+\text{...}+{\text{a}}_{10}=\text{0}$. (Az $\left({\text{a}}_i-\text{p}\right)\times \left({\text{a}}_{i+1}-\text{p}\right)$ vektorok párhuzamosak és azonos állásúak, ezért abszolút értékük összege ‐ a kék háromszögek területösszegének kétszerese ‐ egyenlő az összegük abszolút értékével.)