Feladat: B.3466 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Lovrics Klára 
Füzet: 2002/február, 89 - 93. oldal  PDF  |  MathML 
Témakör(ök): Esetvizsgálat, Mértani helyek, Látókörív, Vektorok, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):Feladatok: 2001/május: B.3466

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha P a négyzet AB vagy CD oldalegyenesén van, akkor a feltétel nyilván nem teljesül. Ha tehát sinAPB∢=sinDPC∢, akkor létezik az A, B, P pontokon átmenő k1 és a C, D, P pontokon átmenő k2 kör. Ezekben a körökben AB és CD egyenlő vagy kiegészítő kerületi szögekkel szemközti húrok. Mivel a négyzet oldalai, ezért egyenlők, így a k1 és k2 körök egybevágók.
Megfordítva, ha P két egybevágó kör közös pontja, amelyek egyike A-n és B-n, a másik pedig C-n és D-n megy át, akkor az APB∢ és DPC∢ egyenlők, vagy pedig 180∘-ra egészítik ki egymást, tehát sinAPB∢=sinDPC∢. A szóban forgó mértani hely tehát az AB-n illetve a CD-n átmenő egybevágó körpárok közös pontjaiként adódik.
Tekintsünk tehát egy tetszőleges k1 kört, amelyik átmegy az A és B pontokon. A C és D pontokon ekkor két olyan kör megy át, amelyik egybevágó a k1-gyel: a k1 tükörképe az AD és BC f felező merőlegesére, illetve az a kör, amelyet úgy kapunk, ha k1-et eltoljuk az AD→=BC→ vektorral. (Az AB szakaszt mindkét transzformáció a CD-be viszi.) Jelöljük a tükrözéssel kapott kört k21-gyel, az eltoltat pedig k22-vel. (Ha k1 éppen az AB átmérőjű kör, akkor k21=k22.)

 
1. eset: k1 és k21 közös pontjai.
Ha a két kör, k1 és k21 nem esik egybe, akkor legfeljebb két közös pontjuk van. Ezek ‐ ha létrejönnek ‐rajta vannak a tükrözés tengelyén. Így az f egyenes pontjait kapjuk, és ennek nyilván minden pontja előáll az f-re tükrös ABP illetve DCP pontokon átmenő egybevágó körök metszéspontjaként. (Ilyen P pontokra egyébként az APB és a DPC szögtartományok is tükrösek az f-re, így a szinuszuk egyenlő.) (1.a., 1.b. ábrák.)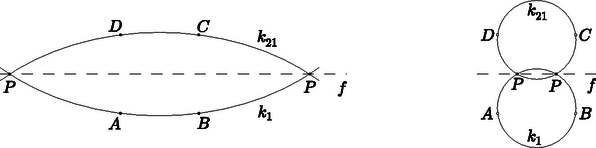

  1.a. ábra  1.b. ábra 

Ha k1 és k21 azonosak, akkor k1=k21 a négyzet körülírt köre. A fentiek szerint ennek a körnek a négyzet csúcsaitól különböző valamennyi pontja a mértani helyhez tartozik (2.a., 2.b. ábrák). A megfordítás most is közvetlenül leolvasható: a P bármely helyzetében negyed- vagy háromnegyed körívnyi kerületi szögek adódnak. Ha P az AB⌢ vagy a CD⌢ íven van, akkor az egyik szög 45∘, a másik pedig 135∘, míg a BC⌢ vagy a DA⌢ íven mindkét szög 45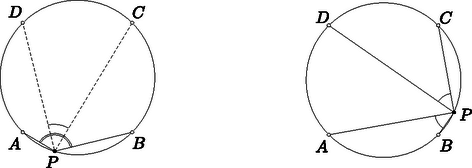∘-os.

 2.a. ábra 2.b. ábra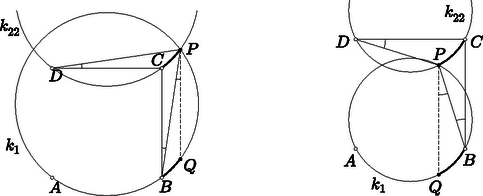 

 
2. eset: k1 és k22 közös pontjai.

 3.a. ábra 3.b. ábra 

A két kör és a négyzet közös szimmetriatengelye az AB felező merőlegese, így a létrejövő két metszéspont közül azt vizsgáljuk, amelyik a B, C pontokkal azonos félsíkban van (3.a., 3.b. ábrák). A k22 kört a k1 eltoltjaként kaptuk, így ha a P-n keresztül párhuzamost húzunk BC-vel, akkor ez a k1 kört abban a Q pontban metszi, amelyre QP→=BC→, az eltolás során éppen a Q pont képe a P. Az eltolás így a k1 kör QB⌢ ívét a k22 kör PC⌢ ívébe viszi. Mivel pedig egybevágó körökben egyenlő ívekhez egyenlő kerületi szögek tartoznak, a k22-beli PDC∢ és a k1-beli QPB∢ egyenlő. A PQBC paralelogrammában pedig QPB∢=CBP∢. A két eredményt egybevetve
PDC∢=CBP∢,
a P pont rajta van a négyzet AC átlóján. (A körök másik metszéspontja az AC átló centrálisra vonatkozó tükörképén, a BD átlón van.)

 4.a. ábra 4.b. ábra 

Megfordítva, az átlók minden pontjára fennáll a szóban forgó egyenlőség. Ha P az AC átló pontja (4.a., 4.b. ábrák), akkor DPC∢=CPB∢. Mivel A, C és P egy egyenesen vannak, külső P pontra CPB∢=APB∢ (4.a. ábra), belső P pontra pedig 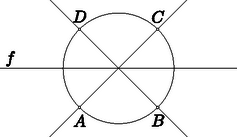CPB∢=180∘-APB∢.

5. ábra

Ezzel minden esetet megvizsgáltunk, a mértani hely a négyzet f szimmetriatengelye, valamint a körülírt kör, továbbá a két átló egyenese a négyzet csúcsainak a kivételével (5. ábra).
 
Megjegyzés. Az egybevágó k1 és k21 illetve k1 és k22 körök metszéspontjainak a vizsgálata koordinátageometriai eszközökkel is történhet. Így okoskodott Ta Vinh Tong, a budapesti Fazekas Mihály Gimnázium 11. osztályos tanulója. A most következő megoldás teljes egészében koordinátageometriai eszközökkel oldja meg a feladatot.

 
II. megoldás. Válasszuk a négyzet oldalát 2 egységnyinek és helyezzük el egy derékszögű koordinátarendszerben úgy, hogy a csúcsok koordinátái legyenek A(-1;-1), B(1;-1), C(1;1), D(-1;1).
Ha P(x,y) tetszőleges pont, akkor a P távolsága az AB egyenestől |y+1|, a CD egyenestől pedig |y-1|. Ha P különbözik az A és B pontoktól, akkor az esetleg elfajuló ABP háromszög területét kétféleképpen fölírva a távolságformula felhasználásával sinAPB∢ kifejezhető:
2TAPB=AP⋅BP⋅sinAPB∢=AB⋅|y+1|,sinAPB=2|y+1|(x+1)2+(y+1)2⋅(x-1)2+(y+1)2
és ugyanígy
sinDPC=2|y-1|(x-1)2+(y-1)2⋅(x+1)2+(y-1)2
Ha P különbözik a négyzet csúcsaitól ‐ ellenkező esetben a szögek valamelyike nem értelmezhető ‐ akkor a fenti kifejezésekben a nevezők értéke nem nulla. A mértani hely egyenlete így
(1)2|y+1|(x+1)2+(y+1)2⋅(x-1)2+(y+1)2==2|y-1|(x-1)2+(y-1)2⋅(x+1)2+(y-1)2.

Emeljük négyzetre (1) két oldalát. Ilyen lépéssel a megoldáshalmaz általában bővül, most azonban nem ez a helyzet. A négyzetre emeléssel kapott egyenlet ugyanis most olyan P pontok megjelenését eredményezi, amelyekre
sinAPB∢=-sinDPC∢.
Ez azt jelenti, hogy a feladat természetes értelmezése szerint konvex APB és DPC szögtartományok mellett az őket 360∘-ra kiegészítő konkáv szögtartományok is megjelennek. Ezek körében a |sinAPB∢|=|sinDPC∢| feltétel ekvivalens a megfelelő konvex szögekre vonatkozó sinAPB∢=sinDPC∢ feltétellel.
Az (x+1)2=a, (x-1)2=b, (y+1)2=c, (y-1)2=d mennyiségek bevezetésével (1) a négyzetre emelés után így alakul:
4c(a+c)(b+c)=4d(a+d)(b+d).
Innen
c(a+d)(b+d)=d(a+c)(b+c).
Az egyenlőség két oldala a változók c↔d cseréjére fölcserélődik, ami azt jelenti, hogy a két oldal különbségéből (c-d) kiemelhető. Valóban beszorzás és rendezés után
cab-dab+cad-dac+cdb-dcb+cd2-dc2=(c-d)(ab-cd)=0.
Visszahelyettesítve:
c-d=(y+1)2-(y-1)2=4yab-cd=(x2-1)2-(y2-1)2=(x2-y2)(x2+y2-2),
a négyzet csúcsaival bővített ponthalmaz egyenlete:
y(x2-y2)(x2+y2-2)=0.
y=0 az x tengely egyenlete, ez a négyzet AD-t és BC-t felező szimmetriatengelye. x2-y2=0 metsző egyenespár, a négyzet két átlójának az egyenlete, végül x2+y2-2=0 a négyzet körülírt körének az egyenlete.
A bizonyításból következik, hogy a négyzet csúcsaitól eltekintve valamennyi pontra teljesül a sinAPB∢=sinDPC∢ feltétel. Ez egyébként közvetlenül is könnyen igazolható a talált pontokra.
A keresett mértani hely így a négyzet BC-re merőleges szimmetriatengelye, a négyzet átlóegyenesei és a négyzet körülírt köre a négy csúcs, A, B, C, D kivételével (5. ábra).
 Lovrics Klára (Budapest, Eötvös József Gimnázium, 12. o.t.)