Kezdőlap


Feladat:	2000. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Béky Bence
Füzet:	2001/február, 67 - 73. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Síkgeometriai bizonyítások, Inverzió, Egyenlő szárú háromszögek geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 2001/február: 2000. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az első két megoldás a körre vonatkozó inverzió fogalmára támaszkodik, ezért röviden összefoglaljuk ennek a transzformációnak legfontosabb tulajdonságait. Ha adott a síkon egy $O$ középpontú, $r$ sugarú $k$ kör, akkor a $k$ körre vonatkozó inverzió a sík $O$ -tól különböző pontjainak az a leképezése, amely tetszőleges $P$ ponthoz az $O P$ félegyenes azon $P'$ pontját rendeli hozzá, amelyre $O P \cdot O P' = r^{2}$ . Ha az $A$ pont (vagy alakzat) képe $B$ , akkor a $B$ ponté (alakzaté) éppen $A$ . A leképezés tehát egy-egyértelmű, a $k$ pontjait helyben hagyja, $k$ -n belüli pontokat pedig $k$ -n kívüli pontokba visz, és fordítva. Ha egy kör az $O$ pontot elkerüli, akkor a körvonal képe egy, az $O$ -t szintén elkerülő körvonal, egy $O$ -n áthaladó $k_{1}$ körvonal képe pedig egy $O$ -ra nem illeszkedő egyenes: a $k$ és $k_{1}$ körök hatványvonala. Fontos tulajdonsága az inverziónak a szögtartás: ha $k_{1}$ és $k_{2}$ egy-egy körvonal (elfajuló esetben $O$ -ra nem illeszkedő egyenes), akkor a $k_{1}'$ és $k_{2}'$ körök ugyanolyan szög alatt metszik egymást, mint a $k_{1}$ és $k_{2}$ körök. (Két egymást metsző kör által bezárt szög alatt közös pontjukban húzott érintőik hajlásszögét értjük.) Speciálisan, ha a $k_{1}$ kör $k$ -t merőlegesen metszi, akkor $k' = k$ miatt $k_{1}'$ is merőlegesen metszi $k$ -t, méghozzá ugyanabban a két pontban, ezért 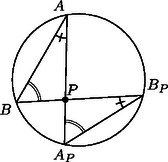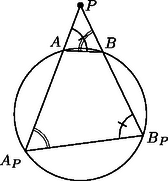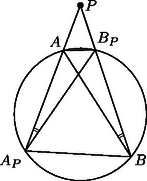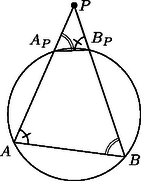$k_{1}' = k_{1}$ .
Ezek után lássuk először a legkevesebb diszkussziót igénylő megoldást.

I. Megoldás. Ha

P

A B C

háromszög köré írható

k

körön van, akkor

A_{P} = B_{P} = C_{P} = P

, és így az

A_{P} B_{P} C_{P}

háromszögről nem beszélhetünk. Az egyazon húrhoz tartozó kerületi szögek egyenlőségéről szóló tételre hivatkozva az 1. ábráról leolvasható, hogy az

A_{P} B_{P} P

háromszög hasonló a

B A P

háromszöghöz, függetlenül attól, hogy

P

k

körön belül, vagy azon kívül helyezkedik-e el. Ezért

\frac{A_{P} B_{P}}{B_{P} P} = \frac{B A}{A P}

, és hasonló módon

\frac{C_{P} B_{P}}{B_{P} P} = \frac{B C}{C P}

1. ábra

A_{P} B_{P} = B_{P} C_{P}

feltétel tehát ekvivalens az

\frac{A P}{C P} = \frac{A B}{C B}

feltétellel, vagyis azzal, hogy

P

A

és

C

pontokhoz, valamint az

\frac{A B}{C B}

arányhoz tartozó Apollóniusz-körnek

k

-ra nem illeszkedő pontja. (Abban a speciális esetben, amikor

A B = C B

, ez az Apollóniusz-kör elfajuló, és az

A C

szakasz felező merőlegesével egyezik meg.) Ugyanígy kapjuk azt is, hogy az

A_{P} B_{P} = A_{P} C_{P}

feltétel ekvivalens azzal, hogy

P

B

és

C

pontokhoz, valamint az

\frac{B A}{C A}

arányhoz tartozó Apollóniusz-körnek

k

-ra nem illeszkedő pontja. Az

A_{P} B_{P} C_{P}

háromszög tehát pontosan akkor szabályos, ha

P

az említett két Apollóniusz-kör (

k

-ra nem illeszkedő) közös pontja.
Az

A C

egyenes elválasztja az első Apollóniusz-kör

k

-val való,

B

-től különböző

B'

metszéspontját a

B

ponttól. Ugyanígy, a

B C

egyenes elválasztja a második Apollóniusz-kör

k

-val való,

A

-től különböző

A'

metszéspontját az

A

ponttól. Következésképpen az

A

B

A'

B'

pontok a

k

körön ilyen sorrendben helyezkednek el (2. ábra), és ezért a két Apollóniusz-kör mind a

k

körön belül, mind azon kívül egy-egy pontban metszi egymást. Pontosabban, a

k

-n kívüli metszéspont nem létezik abban az esetben, ha mind a két Apollóniusz-kör elfajuló, ez azonban pontosan akkor következik be, ha az

A B C

háromszög szabályos. Ezzel a feladat első állítását beláttuk.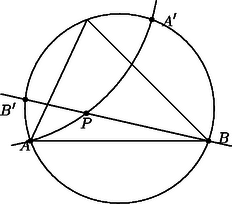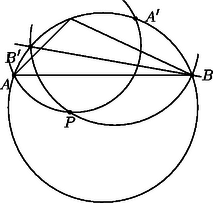

2. ábra

A második állítás bizonyítása azon az észrevételen alapul, hogy az említett Apollóniusz-körök a

k

kört merőlegesen metszik. Ekkor ugyanis a szögtartás miatt a

k

-ra vonatkozó inverzió mind a két Apollóniusz-kört saját magába viszi, és ezért a körök metszéspontjainak képe az inverzió során ugyanez a két pont. Mivel a

k

körön belüli pontok a

k

-n kívüli pontokba transzformálódnak, ez csak úgy lehetséges, ha az inverzió

P

-t és

Q

-t felcseréli. A

P

és

Q

pontok tehát egymásnak a

k

körre vonatkozó inverz képei, ennek megfelelően a

P Q

egyenes valóban áthalad a

k

kör

O

középpontján.

Szimmetria okokból elegendő azt megmutatni, hogy az első Apollóniusz-kör (jelöljük ezt

k_{1}

-gyel) merőlegesen metszi

k

-t. Ez nyilvánvaló, ha

A B = C B

, egyébként pedig feltehetjük, hogy

α = B A C ∢ > B C A ∢ = γ

. Legyen a

B

-ből induló belső szögfelező talppontja

T

, a külsőé

S

. A szögfelező-tétel értelmében

S T

éppen a

k_{1}

körnek az

A C

egyenesre eső átmérője, amely tartalmazza az

A

pontot is (3. ábra).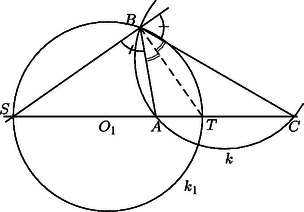

3. ábra

Ezért

S B T ∢ = \frac{π}{2}

. Továbbá

\begin{matrix} T B O ∢ = \frac{β}{2} - (\frac{π}{2} - α) = \frac{π}{2} - (π - (α + \frac{β}{2})) = \frac{π}{2} - B T S ∢ = B S T ∢ = S B O_{1} ∢, \end{matrix}

ahol

O_{1}

k_{1}

kör középpontja. Ezért

\begin{matrix} O_{1} B O ∢ = S B T ∢ + T B O ∢ - S B O_{1} ∢ = \frac{π}{2}, \end{matrix}

és éppen ezt akartuk bizonyítani.

II. Megoldás. Rögzítsük a pozitív forgásirányt úgy hogy az

A

B

C

csúcsok ilyen sorrendben helyezkedjenek el a háromszög köré írt

k

körön. Hogy kevesebb esetet kelljen megkülönböztetni, irányított szögekkel fogunk dolgozni. Két irányított szöget azonosnak tekintünk akkor, ha különbségük

2 π

egész számú többszöröse.
Ha

X

Y

k

kör pontjai, akkor az

X Y

irányított ívhez tartozó (irányított) kerületi szöget jelölje

φ (X Y)

. Például

φ (A B) = γ

ϕ (B C) = α

és

ϕ (C A) = β

a háromszög szögei, ugyanakkor

φ (B A) = 180^{\circ} - γ

. Azt mondjuk, hogy az

X Y

(irányított) szakasz a

P

pontból

ϕ

szög alatt látszik, ha

X P Y ∢ = ϕ

, ekkor az

Y X

szakasz

P

-ből

- ϕ

szög alatt látszik. Az ilyen

P

pontok összessége alkotja az

X Y

szakaszra támaszkodó

ϕ

szögű látókörívet, ami

ϕ = π

esetén a végpontjait nem tartalmazó

X Y

szakasszal,

ϕ = 0

esetén pedig az

X Y

egyenes

X Y

szakaszon kívül eső részével egyezik meg.
Ennyi előkészület után most már rátérhetünk a megoldás lényegi részére. A

k

körön nyilván nem helyezkedhet el megfelelő pont. Legyen tehát először

P

k

kör egy tetszőleges belső pontja, ekkor az

A B C

és

A_{P} B_{P} C_{P}

háromszögek azonos körüljárásúak. Az utóbbi háromszög tehát pontosan akkor szabályos, ha a

ϕ (A_{P} B_{P})

ϕ (B_{P} C_{P})

ϕ (C_{P} A_{P})

szögek közül legalább kettő (és persze akkor a harmadik is)

60^{\circ}

. Mármost

\begin{matrix} \begin{matrix} A P B ∢ = 180^{\circ} - B A P ∢ - P B A ∢ = 180^{\circ} - B A P_{A} ∢ - B_{P} B A ∢ = \\ 180^{\circ} - ϕ (B A_{P}) - ϕ (B_{P} A) = ϕ (A B) + ϕ (A_{P} B_{P}) = γ + ϕ (A_{P} B_{P}), \end{matrix} \end{matrix}

A B

B A_{P}

A_{P} B_{P}

és

B_{P} A

ívek ugyanis együtt éppen lefedik a

k

kört, így a hozzájuk tartozó kerületi szögek összege pontosan

180^{\circ}

. Hasonlóképpen,

B P C ∢ = α + ϕ (B_{P} C_{P})

és

C P A ∢ = β + ϕ (C_{P} A_{P})

. Az

A_{P} B_{P} C_{P}

háromszög tehát pontosan akkor szabályos, ha a

P

pontból az

A B

B C

C A

szakaszok rendre

γ + 60^{\circ}

α + 60^{\circ}

β + 60^{\circ}

szögben látszanak. E három feltétel közül persze elég csak kettőt megkövetelni.
Most már nem nehéz megmutatni, hogy a

k

körön belül pontosan egy ilyen

P

pont van. Az általánosság megszorítása nélkül feltehetjük, hogy

α

γ < 120^{\circ}

. Tekintsük most az

A B

szakaszra támaszkodó

γ + 60^{\circ}

szögű

ℓ_{C}

látókörívet és a

B C

szakaszra támaszkodó

α + 60^{\circ}

szögű

ℓ_{A}

látókörívet, ezek tehát a megfelelő szakaszoknak a háromszöget tartalmazó oldalán helyezkednek el. A harmadik hasonló látókörívre is (amely már nem biztos, hogy az AC szakasznak a háromszöget tartalmazó oldalán helyezkedik el) szükségünk lesz később, ezt jelöljük

ℓ_{B}

-vel. Hogy ez a két ív pontosan egy pontban metszi egymást, méghozzá a

k

kör belsejében, a következőképpen igazolhatjuk. Először is vegyük észre, hogy mindkét látókörív a

k

kör belsejében halad. Másodszor,

B

közös végpontja mindkét ívnek. Ezért a két ívnek legfeljebb egy közös belső pontja lehet, és a metszéspont létrejöttének szükséges és elégséges feltétele az, hogy az

ℓ_{A}

ív a

B C

oldallal, illetve az

ℓ_{C}

ív a

B A

oldallal olyan szögeket zárjon be, amelyek összege

β

-t meghaladja (most kivételesen nem irányított szögektől beszélünk). Egyszerű számolással ellenőrizhető, hogy ez valóban így van. Azt is megállapíthatjuk, hogy lévén ekkor

C P A ∢ = β + 60^{\circ}

, ez a

P

pont akkor esik az

A B C

háromszög belsejébe, ha

β < 120^{\circ}

, a háromszögön kívül helyezkedik el a

β > 120^{\circ}

esetben, ha pedig

β = 120^{\circ}

, akkor az

A C

oldalra illeszkedik.
Összefoglalva tehát megállapíthatjuk, hogy a

k

körön belül mindig pontosan egy ilyen pont van, méghozzá az

A B C

háromszög belsejében, ha a háromszög minden szöge

120^{\circ}

-nál kisebb, annak határán, ha a háromszögnek van egy

120^{\circ}

-os szöge, illetve azon kívül, ha valamelyik szöge

120^{\circ}

-nál nagyobb. Ebből a

P

pontból az

A B

B C

C A

szakaszok rendre

γ + 60^{\circ}

α + 60^{\circ}

β + 60^{\circ}

alatt látszanak.
Legyen most a

P

pont a

k

kör egy külső pontja. Az

A P B ∢

meghatározásához különböztessünk meg négy esetet annak megfelelően, hogy a

P A

és

P B

félegyeneseken a

P

A

A_{P}

, illetve

P

B

B_{P}

pontok milyen sorrendben helyezkednek el (1. ábra). Megjegyezzük, hogy az irányított szögekkel való számolásnak az is előnye, hogy nem kell azzal foglalkoznunk, hogy ez a két félegyenes egymáshoz képest milyen helyzetű. Mind a négy esetben könnyen ellenőrizhető, hogy

\begin{matrix} A P B ∢ = 180^{\circ} - B A P ∢ - P B A ∢ = 180^{\circ} - ϕ (B A_{P}) - ϕ (B_{P} A) = \end{matrix}

\begin{matrix} (180^{\circ} - ϕ (B A_{P}) - ϕ (A_{P} A)) - ϕ (B_{P} A_{P}) = ϕ (A B) - ϕ (B_{P} A_{P}) = γ - ϕ (B_{P} A_{P}) . \end{matrix}

Ugyanígy

B P C ∢ = α - ϕ (C_{P} B_{P})

és

C P A ∢ = β - ϕ (A_{P} C_{P})

. Mivel most az

A_{P} B_{P} C_{P}

háromszög körüljárása ellentétes az

A B C

háromszögével, ez a háromszög pontosan akkor szabályos, ha a

ϕ (B_{P} A_{P})

ϕ (C_{P} B_{P})

ϕ (A_{P} C_{P})

szögek közül legalább kettő (és persze akkor a harmadik is)

60^{\circ}

. Ezzel ekvivalens az, hogy a

P

pontból az

A B

B C

C A

szakaszok rendre

γ - 60^{\circ}

α - 60^{\circ}

és

β - 60^{\circ}

alatt látszanak. Jelölje az ennek megfelelő látóköríveket rendre

ℓ_{C}'

ℓ_{A}'

és

ℓ_{B}'

.
Állítás. A

k

körre vonatkozó inverziónál az

ℓ_{A}

ℓ_{B}

ℓ_{C}

ívek képe rendre

ℓ_{A}'

ℓ_{B}'

és

ℓ_{C}'

.
Ebből azonnal következik, hogy a

k

körön kívül is pontosan egy olyan

Q

pont van, amelyre az

A_{Q} B_{Q} C_{Q}

háromszög szabályos, mégpedig ez a pont a

P

pont inverz képe. Probléma csak akkor lenne, ha

P

egybeesne a

k

kör középpontjával, ez azonban nem lehetséges, hiszen az

A B C

háromszög nem szabályos. Egyúttal azt is megkaptuk, hogy a

k

kör középpontja, valamint a

P

és

Q

pontok egy egyenesen vannak.
Most már csak a fenti állítást kell igazolni. Ha a háromszög szögeire semmiféle megkötést nem teszünk, akkor szimmetria okok miatt nyilván elég annyit megmutatni, hogy

ℓ_{A}

inverz képe éppen

ℓ_{A}'

. A bizonyítás azon az egyszerű észrevételen múlik, hogy az a két ív, amelynek pontjaiból az

X Y

(irányított) szakasz

ϕ_{1}

, illetve

ϕ_{2}

szög alatt látszik,

ϕ_{1} - ϕ_{2}

szöget zár be egymással. Ennek alapján a kerületi szögek tételéből következik, hogy mind az

ℓ_{A}

ív, mind az

ℓ_{A}'

ív

60^{\circ}

-os szöget zár be a

k

körrel. Nem nehéz megmutatni, hogy az

ℓ_{A}

ív a

k

körön belül, az

ℓ_{A}'

ív pedig azon kívül halad. A két ívnek ugyanazok a végpontjai, de nem egészítik ki egymást egyetlen körvonallá. Mivel az a két körvonal, amely a

k

-t a

B

és

C

pontokban egyaránt

60^{\circ}

-os szög alatt metszi, egymás inverz képe a

k

körre nézve, a szóban forgó két ív is egymás inverze, és ezt akartuk bizonyítani.

III. Megoldás. (Béky Bence megoldása.) Az előző megoldások valamelyikét követve először is megállapítjuk, hogy valóban két ilyen pont létezik, méghozzá egy a háromszög köré írható körön belül (jelöljük ezt

P

-vel), a másik pedig a körön kívül (legyen ez

Q

). Vegyük most észre, hogy az

A_{P} B_{P} C_{P}

háromszög körüljárása megegyezik az

A B C

háromszögével, míg az

A_{Q} B_{Q} C_{Q}

háromszögé azzal ellentétes. Található tehát egy, a

k

kör

O

középpontjára illeszkedő

e

egyenes, amelyre az

A_{P} B_{P} C_{P}

háromszöget tükrözve az

A_{Q} B_{Q} C_{Q}

háromszöget kapjuk.
Vizsgáljuk először azt az általános esetet, amikor

A_{P}

különbözik a

B_{Q}

C_{Q}

pontoktól,

B_{P}

különbözik az

A_{Q}

C_{Q}

pontoktól és

C_{P}

is különbözik az

A_{Q}

B_{Q}

pontoktól. Nem lehet, hogy például az

A_{P} B_{Q}

egyenes egybeesik az

A_{Q} B_{P}

egyenessel, mert ekkor

A_{P} = B_{P}

lenne. Az

A_{P} B_{Q}

egyenes tehát csak akkor lehet párhuzamos az

A_{Q} B_{P}

egyenessel, ha egyben

e

-vel is párhuzamos. Ugyanez elmondható a másik két értelemszerűen felírt egyenespárról. Jelölje

A^{*}

B^{*}

és

C^{*}

rendre a

B_{P} C_{Q}

és

B_{Q} C_{P}

egyeneseknek, az

A_{P} C_{Q}

és

A_{Q} C_{P}

egyeneseknek, illetve az

A_{P} B_{Q}

és

A_{Q} B_{P}

egyeneseknek a metszéspontját. Az elmondottak szerint ezen egyenespárok közül legfeljebb egy lehet párhuzamos helyzetben, az

e

egyenesre eső

A^{*}

B^{*}

C^{*}

pontok közül tehát kettő biztosan létrejön. Feltehetjük, hogy az

A^{*}

és

B^{*}

pontok ilyenek. Világos, hogy

A^{*}

és

B^{*}

különböző pontok (4. ábra).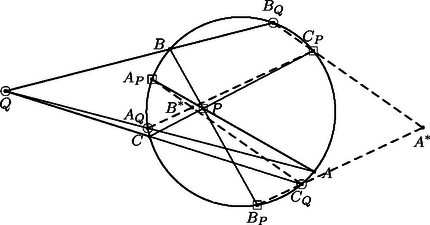

4. ábra

Tekintsük most a

k

körbe írt

B B_{Q} C_{P} C C_{Q} B_{P}

önmagát átmetsző hatszöget. Ennek

B B_{Q}

és

C C_{Q}

szemközti oldalai

Q

-ban,

B_{Q} C_{P}

és

C_{Q} B_{P}

szemközti oldalai

A^{*}

-ban,

C_{P} C

és

B_{P} B

szemközti oldalai pedig

P

-ben metszik egymást. Pascal tétele szerint tehát az

A^{*}

pont illeszkedik a

P Q

egyenesre (5. ábra).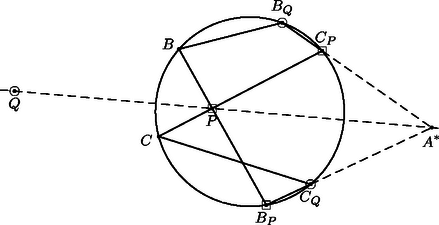

5. ábra

Hasonlóképpen belátható, ezúttal az

A A_{Q} C_{P} C C_{Q} A_{P}

hatszögből kiindulva, hogy a

B^{*}

pont is illeszkedik a

P Q

egyenesre. A

P Q

egyenes tehát egybeesik az

A^{*} B^{*}

egyenessel, vagyis az

O

ponton áthaladó

e

egyenessel, ami bizonyítja az általános esetben a feladat második állítását.
Tegyük fel végül, hogy mondjuk

B_{P} = C_{Q} = X

, ekkor az

e

-re való szimmetria miatt

B_{Q} = C_{P} = Y

, végül pedig

A_{P} = A_{Q}

k

körnek az a

Z

pontja, amelyre az

X Y Z

háromszög szabályos. Világos, hogy

Z

illeszkedik az

e

egyenesre,

X Y

pedig merőleges arra. Ekkor az

B_{P} C_{Q}

és

B_{Q} C_{P}

egyenesek helyett tekintsük a

k

körhöz annak

X

, illetve

Y

pontjában húzott érintőjét, ez a két egyenes a

Z

pontnak az

X Y

-ra vonatkozó tükörképében metszi egymást. Jelöljük most ezt a pontot

A^{*}

-gal. A

B^{*}

C^{*}

pontok ugyanúgy definiálhatók, mint az általános esetben, és ezúttal egybeesnek

Z

-vel. Az

A^{*}

és

B^{*}

pontok tehát most is az

e

egyenest határozzák meg. Most már szinte szó szerint megismételhetjük az előző bekezdést azzal az apró módosítással, hogy most a

B B_{Q} C_{P} C C_{Q} B_{P}

hatszög elfajuló abban az értelemben, hogy két-két szomszédos csúcsa egybeesik. Ezért a Pascal tétel alkalmazásánál a

B_{P} C_{Q}

és

B_{Q} C_{P}

egyenesek helyett éppen az előbb említett érintőket kell tekinteni.

Megjegyzések. 1. A feladat komplex számok segítségével viszonylag egyszerű számolás útján is megoldható. Ezt az utat választotta Gyenes Zoltán a második állítás bizonyításához.
2. Egy mélyebb matematikai eszközöket használó megoldást tartalmaz, és a feladat hátterére mutat rá Hraskó András cikke, amely a következő számunkban jelenik meg.
3. A harmadik megoldásból azonnal leolvasható, hogy az

A_{P} B_{P} C_{P}

és

A_{Q} B_{Q} C_{Q}

háromszögek a

P Q

egyenesre szimmetrikusan helyezkednek el. Erre az eredményre az első megoldás ügyes folytatásával is eljuthatunk. Hogyan? Ennek az önmagában is szép feladatnak a megoldását már az olvasóra bízzuk.