Feladat:	B.3358	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2001/február, 95 - 97. oldal		PDF  |  MathML
Témakör(ök):	Egyenlőtlenségek, Geometriai egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2000/március: B.3358

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $a$ rögzített valós szám, és tekintsük az $f_a\left(x\right)=\frac{1+ax}{\sqrt[]{1+a^2}\sqrt[]{1+x^2}}$ függvényt. $f_a$ minden valós számra értelmes, és mint az szokványos eszközökkel (elemi differenciálszámítással) megmutatható, $f_a$ a $\left(-\infty ;a\right]$ intervallumon növő, az $\left[a;+\infty \right)$ intervallumon fogyó, $\underset{+\infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}{f}_a=\frac{a}{\sqrt[]{1+a^2}}$ és $\underset{-\infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}{f}_a=-\frac{a}{\sqrt[]{1+a^2}}$. Ezzel a jelöléssel adott $a$ és $b$ számokra pontosan akkor teljesül a feladat előírása, ha $f_a\left(b\right)>\frac{1}{2}$. Az 1.a), b) ábrán az $f_a$ grafikonja látható $a>0$, illetve $a<0$ esetben. Könnyű számolással kapjuk, hogy ha $|a|\ge \frac{\sqrt[]{3}}{3}$, akkor $\frac{|a|}{\sqrt[]{1+a^2}}\ge \frac{1}{2}$. Így ha $a\ge \frac{\sqrt[]{3}}{3}$, akkor $f_a\left(x\right)>\frac{1}{2}$ minden $x\ge a$ esetén, ha pedig $a\le -\frac{\sqrt[]{3}}{3}$, akkor $f_a\left(x\right)>\frac{1}{2}$ minden $x\le a$ esetén. Ez azt jelenti, hogy ha a négy adott valós szám közül kettő esik akár a $\left[\frac{\sqrt[]{3}}{3};+\infty \right)$, akár pedig a $\left(-\infty ;-\frac{\sqrt[]{3}}{3}\right]$ intervallumba, akkor teljesül rájuk az előírt egyenlőtlenség. Ha egyik fenti intervallumban sincs egynél több a megadott számok közül, akkor legalább kettő esik a $\left(-\frac{\sqrt[]{3}}{3};\frac{\sqrt[]{3}}{3}\right)$ intervallumba. Egyszerű számolással kapjuk, hogy $f_a\left(\frac{\sqrt[]{3}}{3}\right)>\frac{1}{2}$ pontosan akkor teljesül, ha $a>-\frac{\sqrt[]{3}}{3}$. Így ha $-\frac{\sqrt[]{3}}{3}<a\le b<\frac{\sqrt[]{3}}{3}$, akkor $\begin{array}{c}{\displaystyle 1=f_a\left(a\right)\ge f_a\left(b\right)>f_a\left(\frac{\sqrt[]{3}}{3}\right)>\frac{1}{2}\mathrm{,}}\end{array}$ hiszen az $f$ szigorúan monoton fogyó az $\left[a;+\infty \right)$ intervallumon. Ezzel megmutattuk, hogy négy valós szám között valóban mindig található kettő, amelyekre teljesül az előírt egyenlőtlenség.   II. megoldás. Némi tapasztalat és intuíció révén természetes jelentés adható az egyenlőtlenség bal oldalán szereplő kétváltozós kifejezésnek, továbbá ‐ ennek nyomán ‐ maga az állítás is egy geometriai közhellyé egyszerűsödik. A nevezőben álló pitagoraszi mennyiségek nyomán természetesnek látszik az $A\left(1;a\right)$ és a $B\left(1;b\right)$ pontok bevezetése (2. ábra). A koszinusztételt az $OAB$ háromszögben felírva: $\begin{array}{c}{\displaystyle {\left(a-b\right)}^2=\left(1+a^2\right)+\left(1+b^2\right)-2\sqrt[]{1+a^2}\sqrt[]{1+b^2}\text{cos}AOB\sphericalangle \mathrm{,}}\end{array}$ ahonnan rendezés után $\text{cos}AOB\sphericalangle =\frac{1+ab}{\sqrt[]{1+a^2}\sqrt[]{1+b^2}}$, a szóban forgó egyenlőtlenség bal oldala adódik, maga a feltétel pedig a $\begin{array}{c}{\displaystyle \text{cos}AOB>\frac{1}{2}\mathrm{,}\text{azaz az}AOB\sphericalangle <{60}^{\circ }}\end{array}$ alakot ölti. Ebben a formában az állítás azt jelenti, hogy ha adott négy pont az $x=1$ egyenesen, akkor van köztük kettő, $A$ és $B$, hogy $AOB\sphericalangle <{60}^{\circ }$. Ez pedig nyilvánvaló, az $O$ pontból kiinduló $\frac{\sqrt[]{3}}{3}$ és $-\frac{\sqrt[]{3}}{3}$ meredekségű félegyenesek a nyílt pozitív félsíkot három ${60}^{\circ }$-os szögtartományra osztják, a középső nyílt, a két szélső pedig félig nyílt, így a skatulyaelv szerint a négy adott pont között van olyan kettő, amelyik ugyanannak a tartománynak a belsejében található (3. ábra). Erre a két pontra pedig az $AOB$ szög kisebb, mint ${60}^{\circ }$.     Megjegyzések. 1. A két megoldás kapcsolata jól látható, a második jelentése mintegy értelmezi az első függvényének a viselkedését, az ott kapott eredmények a geometriai megközelítésben érthetők meg. A feladat persze korrekt módon oldható meg az első megoldás módszerével, legfeljebb az az érzésünk, hogy egy sötét szobában kerestük a kijáratot a falak mentén tapogatva ‐ és meg is találtuk ‐, míg a második megoldásban először a lámpát kapcsoltuk fel. Ez mindig látványos, de jó tudni, hogy akkor sem kell kétségbe esni, ha nem találjuk a kapcsolót. 2. A második megoldás ötletéhez az $\text{a}\left(1;a\right)$ és $\text{b}\left(1;b\right)$ vektorok skalárszorzata, $1+ab$, illetve a definícióból adódó $\text{cos}\phi =\frac{\text{a}\cdot \text{b}}{|\text{a}||\text{b}|}$ alak felismerése közvetlenül is elvezethet, egyúttal rámutathatunk a feladat lehetséges eredetére.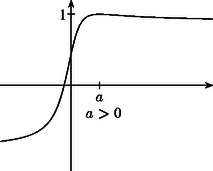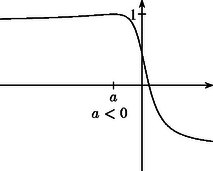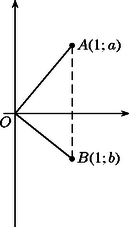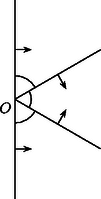