Kezdőlap


Feladat:	B.3379	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2001/január, 32 - 34. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Síkgeometriai számítások trigonometria nélkül, Körülírt kör, Beírt kör, Szögfelező egyenes, Feladat
Hivatkozás(ok):	Feladatok: 2000/május: B.3379

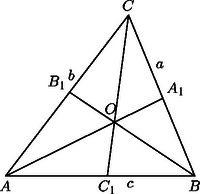
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög oldalait a szokásos módon $a$ , $b$ , $c$ -vel, területét $T$ -vel, kerületének felét pedig $s$ -sel.
Először kifejezzük az egyenlőtlenség középső tagjában szereplő arányokat a háromszög oldalaival. Az $A B A_{1}$ háromszögben $B O$ szögfelező, ezért a szögfelezőtétel szerint a szemközti oldalt a mellette levő oldalak arányában osztja, vagyis

\begin{matrix} \frac{A O}{A_{1} O} = \frac{A B}{A_{1} B} . \end{matrix}

(1)

A A_{1}

egyenes a

C A B

háromszögben szögfelező, ezért

\begin{matrix} \frac{A_{1} B}{A_{1} C} = \frac{c}{b} . \end{matrix}

(2)

A_{1} B + A_{1} C = a

, vagyis

A_{1} C = a - A_{1} B

, amit (2)-be helyettesítve, majd a kapott egyenlőségből

A_{1} B

-t kifejezve

\begin{matrix} A_{1} B = \frac{a \cdot c}{b + c} . \end{matrix}

Ezt (1)-be beírva kapjuk, hogy

\begin{matrix} \frac{A O}{A_{1} O} = \frac{A B}{A_{1} B} = \frac{c}{\frac{a \cdot c}{b + c}} = \frac{b + c}{a} . \end{matrix}

Ugyanígy látható be, hogy

\begin{matrix} \frac{B O}{B_{1} O} = \frac{a + c}{b} és \frac{C O}{C_{1} O} = \frac{a + b}{c} . \end{matrix}

Ismert, hogy

R = \frac{a b c}{4 T}

r = \frac{T}{s}

és

T^{2} = s (s - a) (s - b) (s - c)

. Ezeket az összefüggéseket felhasználva a

4 R / r

hányadost is kifejezhetjük az oldalakkal:

\begin{matrix} \frac{4 R}{r} = \frac{\frac{a b c}{T}}{\frac{T}{s}} = \frac{a b c \cdot \frac{a + b + c}{2}}{\frac{a + b + c}{2} \cdot \frac{b + c - a}{2} \cdot \frac{a - b + c}{2} \cdot \frac{a + b - c}{2}} = \frac{8 a b c}{(b + c - a) (a - b + c) (a + b - c)} . \end{matrix}

A bizonyítandó egyenlőtlenségek tehát az oldalakkal kifejezve:

\begin{matrix} 8 \leq \frac{(a + b) (a + c) (b + c)}{a b c} \leq \frac{8 a b c}{(b + c - a) (a - b + c) (a + b - c)} . \end{matrix}

(3)

A számtani és a mértani közepek közötti egyenlőtlenség szerint

2 \sqrt[]{a b} \leq a + b

2 \sqrt[]{b c} \leq b + c

és

2 \sqrt[]{a c} \leq a + c

. Ezeket összeszorozva éppen a bizonyítandó bal oldali egyenlőtlenséggel ekvivalens

\begin{matrix} 8 a b c \leq (a + b) (b + c) (a + c) \end{matrix}

egyenlőtlenséget kapjuk.
A jobb oldali egyenlőtlenséget is három egyenlőtlenség összeszorzásával kaphatjuk. Ezek:

\begin{matrix} \begin{matrix} \frac{a + b}{c} & \leq \frac{2 \sqrt[]{a b}}{\sqrt[]{(b + c - a) (a - b + c)}}, \\ \frac{b + c}{a} & \leq \frac{2 \sqrt[]{b c}}{\sqrt[]{(a - b + c) (a + b - c)}} és & (4) \\ \frac{c + a}{b} & \leq \frac{2 \sqrt[]{a c}}{\sqrt[]{(b + c - a) (a + b - c)}} . \end{matrix} \end{matrix}

Az oldalak szerepe a három egyenlőtlenségben szimmetrikus, ezért közülük elég csak egyet bebizonyítanunk. Az elsőt négyzetre emelve és átszorozva:

\begin{matrix} \begin{matrix} {(a + b)}^{2} (b + c - a) (a - b + c) & \leq 4 a b c^{2}, azaz \\ {(a + b)}^{2} (c^{2} - {(a - b)}^{2}) & \leq 4 a b c^{2} . \end{matrix} \end{matrix}

Ezt rendezve:

\begin{matrix} \begin{matrix} c^{2} ({(a + b)}^{2} - 4 a b) & \leq {(a + b)}^{2} {(a - b)}^{2}, vagyis \\ c^{2} {(a - b)}^{2} & \leq {(a + b)}^{2} {(a - b)}^{2} \end{matrix} \end{matrix}

adódik, ami nyilván igaz, mert a háromszög-egyenlőtlenség miatt

c^{2} < {(a + b)}^{2}

;

{(a - b)}^{2}

pedig nemnegatív. Tehát teljesülnek a (4) egyenlőtlenségek, s így az összeszorzásukkal kapható, (3) jobb oldalán lévő egyenlőtlenség is.
Könnyen látható, hogy mindkét bizonyított egyenlőtlenségben pontosan akkor van egyenlőség, ha

a = b = c

, azaz ha az

A B C

háromszög szabályos.