Feladat:	C.615	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	2001/december, 526 - 527. oldal		PDF  |  MathML
Témakör(ök):	Elsőfokú (és arra visszavezethető) egyenletrendszerek, C gyakorlat
Hivatkozás(ok):	Feladatok: 2001/február: C.615

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.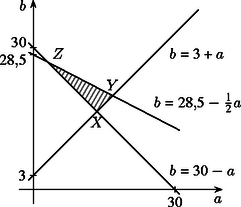   I. megoldás. A zenemű 3 tételének hosszát jelölje $a$, $b$, $c$ úgy, hogy $a<b<c$ legyen; $a+b+c=60$ szerint $c=60-a-b$. Egyik tétel sem hosszabb, mint a másik kettő együttvéve; esetünkben ez azt jelenti, hogy $60-a-b=c\le a+b$, azaz $a+b\ge 30$. A különbségek mindegyike legalább 3, vagyis $b\ge a+3$ és $60-a-b=c\ge b+3$. Így a feladat feltételei a következő egyenlőtlenségekkel írhatók le: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle b}& {\displaystyle \ge 30-a}\hfill & \hfill {\displaystyle \left(1\right)}\\ \hfill {\displaystyle b}& {\displaystyle \ge 3+a}\hfill & \hfill {\displaystyle \left(2\right)}\\ \hfill {\displaystyle b}& {\displaystyle \le \mathrm{28,5}-\frac{1}{2}a}\hfill & \hfill {\displaystyle \left(3\right)}\end{array}}}\end{array}$     Ábrázoljuk ezeket az összefüggéseket az $a$; $b$ koordináta-rendszerben (ábra). A lehetséges $a$, $b$ értékpárok a megfelelő tartományok közös részébe (a jelölt háromszögbe) eső pontok koordinátái, ezért az $X$, $Y$, $Z$ pontok koordinátáinak kiszámításával megkaphatjuk a legrövidebb tétel hosszának korlátait. Látható, hogy a $Z$ pont első koordinátája szolgáltatja a lehető legkisebb, az $Y$ ponté pedig a lehető legnagyobb $a$ értéket. Az $Y$ pont koordinátái a $\begin{array}{c}{\displaystyle b=3+a\mathrm{,}b=\mathrm{28,5}-\mathrm{0,5}a}\end{array}$ egyenletrendszer megoldása: $Y\left(17;20\right)$. A $Z$ pont koordinátái pedig a $\begin{array}{c}{\displaystyle b=30-a2b=57-a}\end{array}$ egyenletrendszer megoldásából adódnak: $Z\left(3;27\right)$. Ezek alapján a legrövidebb tétel hossza legalább 3, legfeljebb 17 perc lehet, azaz $3\le a\le 17$.   II. megoldás. Ha a három tétel hossza $a<b<c$, és ezek között a különbség páronként legalább 3, akkor $a+3\le b\le c-3$ és $a+3+b+c-3=60$ miatt $a+3$ legfeljebb 20, így $a\le 17$. Tudjuk, hogy $b\le c-3$, azaz $3\le c-b$. A $c\le a+b$ feltételből (egyik tétel sem hosszabb, mint a másik kettő együtt) viszont $c-b\le a$ következik, így $3\le c-b\le a$, tehát $3\le a$, az előző eredménnyel együtt eszerint $3\le a\le 17$. Be kell még látni, hogy ezek a szélsőértékek valóban határok, nemcsak korlátok, keresünk egy-egy példát mindkettőre: $a=17$, $b=20$, $c=23$, illetve $a=3$, $b=27$, $c=30$. (A példák egyébként a konstrukcióból azonnal adódnak.)   Megjegyzés. Nem használtuk a $\left(0<\right)a<b<c$-ből triviálisan adódó $a\le b+c$ és $b\le c+a$ feltételeket. Tetszőleges $3\le a\le 17$ esetén $b$ és $c$ egy lehetséges értéke: $b=\frac{57-a}{2}$, $c=\frac{63-a}{2}$.