Feladat:	B.3470	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Babos Attila ,  Balka Richárd ,  Bóka Gergely ,  Boros Vazul ,  Horváth 424 Márton ,  Horváth Illés ,  Kármán Péter ,  Lovrics Anna ,  Pallos Péter ,  Rácz Béla András ,  Ta Vinh Thong
Füzet:	2001/október, 413 - 416. oldal		PDF  |  MathML
Témakör(ök):	Függvények ábrázolása, Negyed- és magasabb fokú függvények, Függvénytranszformációk, Feladat
Hivatkozás(ok):	Feladatok: 2001/május: B.3470

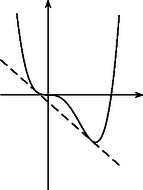
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az $f\left(x\right)=3x^4-4x^3$ függvény grafikonja az 1. ábrán látható, szaggatott vonallal rajzoltuk meg a keresett egyenest. Vegyük észre, hogy ha a szóban forgó polinomokon elvégezzük az $x\leftarrow x+\frac{1}{3}$ helyettesítést ‐ grafikusan ez azt jelenti, hogy a görbét eltoljuk az $x$ tengely mentén $-\frac{1}{3}$ egységgel ‐, akkor a kapott $f_1\left(x\right)=f\left(x+\frac{1}{3}\right)$ negyedfokú polinom nem tartalmaz harmadfokú tagot: ${}^{*}$Ezt az ‐ úgynevezett Tschirnhaus-féle ‐ helyettesítést alkalmazzák az általános negyedfokú egyenlet megoldásának első lépéseként is a harmadfokú tag kiküszöbölésére. $\begin{array}{c}{\displaystyle f_1\left(x\right)=3{\left(x+\frac{1}{3}\right)}^4-4{\left(x+\frac{1}{3}\right)}^3=3x^4-2x^2-\frac{8}{9}x-\frac{1}{9}\mathrm{.}}\end{array}$   $f_1\left(x\right)$-ben a páros fokú tagokat teljes négyzetté alakítva kapjuk, hogy $\begin{array}{c}{\displaystyle f_1\left(x\right)=3{\left(x^2-\frac{1}{3}\right)}^2-\frac{8}{9}x-\frac{4}{9}\mathrm{.}}\end{array}$ Az $y=3{\left(x^2-\frac{1}{3}\right)}^2$ 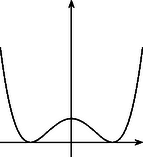grafikonját (2. ábra) nyilván az $x$ tengely érinti kétszer, így az $f_1\left(x\right)$ grafikonjának kettős érintője $y=-\frac{8}{9}x-\frac{4}{9}$. A keresett egyenest most már az inverz $x\leftarrow x-\frac{1}{3}$ helyettesítéssel kapjuk; egyenlete: $\begin{array}{c}{\displaystyle y=-\frac{8}{9}\left(x-\frac{1}{3}\right)-\frac{4}{9}=-\frac{8}{9}x-\frac{4}{27}\mathrm{.}}\end{array}$   II. megoldás. Az $y=ax+b$ egyenletű egyenes pontosan akkor érinti két pontban az $y=3x^4-4x^3$ függvény grafikonját, ha a $p\left(x\right)=3x^4-4x^3-ax-b$ polinom grafikonja két helyen érinti az $x$ tengelyt, azaz két többszörös gyöke van. A görbe negyedfokú, ezért mindkét többszörös gyök kétszeres, több gyöke nincsen, így ha a gyökök $x_1$ és $x_2$, akkor a $p\left(x\right)$ gyöktényezős alakja $\begin{array}{c}{\displaystyle p\left(x\right)=3{\left(x-x_1\right)}^2{\left(x-x_2\right)}^2\mathrm{.}}\end{array}$ (*) A jobb oldalon a műveleteket elvégezve: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 3x^4-4x^3-ax-b=}\\ \hfill {\displaystyle =3x^4-6\left(x_1+x_2\right)x^3+3\left(x_1^2+4x_1{x}_2+x_2^2\right)x^2-6x_1{x}_2\left(x_1+x_2\right)x+3x_1^2{x}_2^2\mathrm{.}}\end{array}}}\end{array}$ Az együtthatók egyenlőségéből $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_1+x_2}& {\displaystyle =\frac{2}{3}\mathrm{,}}\hfill & \hfill {\displaystyle \left(1\right)}\\ \hfill {\displaystyle x_1^2+4x_1{x}_2+x_2^2}& {\displaystyle =\mathrm{0,}}\hfill & \hfill {\displaystyle \left(2\right)}\\ \hfill {\displaystyle 6x_1{x}_2\left(x_1+x_2\right)}& {\displaystyle =a\mathrm{,}}\hfill & \hfill {\displaystyle \left(3\right)}\\ \hfill {\displaystyle -3x_1^2{x}_2^2}& {\displaystyle =b\mathrm{.}}\hfill & \hfill {\displaystyle \left(4\right)}\end{array}}}\end{array}$ (2)-ből ${\left(x_1+x_2\right)}^2=-2x_1{x}_2$, azaz (1) felhasználásával $x_1{x}_2=-\frac{2}{9}$. Innen (3)-ból $a=-\frac{8}{9}$, (4)-ből pedig $b=-\frac{4}{27}$. A keresett egyenes egyenlete tehát csak $y=-\frac{8}{9}x-\frac{4}{27}$ lehet, ez az egyenes pedig valóban megoldás, ugyanis az (1), (2) egyenletekből álló rendszer megoldásai valós számok ($x_1=\frac{1}{3}-\frac{\sqrt[]{3}}{3}$ és $x_2=\frac{1}{3}+\frac{\sqrt[]{3}}{3}$), és így a fenti lépések megfordíthatók, a $\left(*\right)$ szorzat tényezői valós együtthatós polinomok.  Rácz Béla András (Fazekas M. Főv. Gyak. Gimn., 9. o.t.)   III. megoldás. Ha $a$ tetszőleges valós szám, akkor a görbét az $\left(a;f\left(a\right)\right)$ pontjában érintő egyenes egyenlete $\begin{array}{c}{\displaystyle y=f\text{'}\left(a\right)\left(x-a\right)+f\left(a\right)\mathrm{.}}\end{array}$ Ha $b\ne a$, akkor a $\left(b;f\left(b\right)\right)$-beli érintő pontosan akkor lesz ugyanez az egyenes, ha $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle f\text{'}\left(a\right)}& {\displaystyle =f\text{'}\left(b\right)}\hfill & \hfill {\displaystyle \left(1\right)}\\ \hfill {\displaystyle f\left(a\right)-a\cdot f\text{'}\left(a\right)}& {\displaystyle =f\left(b\right)-b\cdot f\text{'}\left(b\right)\mathrm{.}}\hfill & \hfill {\displaystyle \left(2\right)}\end{array}}}\end{array}$ (1)-ből $a-b\ne 0$-val osztva kapjuk, hogy $\begin{array}{c}{\displaystyle a^2+ab+b^2-a-b=\mathrm{0,}}\end{array}$ (3) (2)-ből pedig ugyanígy, hogy $\begin{array}{c}{\displaystyle 9\left(a+b\right)\left(a^2+b^2\right)-8\left(a^2+ab+b^2\right)=0.}\end{array}$ (4) (3) szerint $a^2+ab+b^2=a+b$; ezt felhasználva, (4)-ből $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle a^2+b^2}& {\displaystyle =\frac{8}{9}\mathrm{,}}\hfill & \hfill {\displaystyle \left(5\right)}\\ \multicolumn{3}{c}{\text{<br>amit (3)-ba helyettesítve}}\\ \hfill {\displaystyle a+b-ab}& {\displaystyle =\frac{8}{9}\mathrm{.}}\hfill & \hfill {\displaystyle \left(6\right)}\end{array}}}\end{array}$ Az (5), (6) egyenletrendszer közvetlenül negyedfokú egyenletre vezet; mivel mindkét egyenlet szimmetrikus, érdemes bevezetni az $u=a+b$, $v=ab$ új ismeretleneket: így az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle u^2-2v}& {\displaystyle =\frac{8}{9}\mathrm{,}}\hfill \\ \hfill {\displaystyle u-v}& {\displaystyle =\frac{8}{9}}\hfill \end{array}}}\end{array}$ egyenletrendszerhez, és innen $v=u-\frac{8}{9}$ helyettesítésével az $u^2-2u+\frac{8}{9}=0$ egyenlethez jutunk. Ennek gyökei $u_1=\frac{2}{3}$, $u_2=\frac{4}{3}$. Ennek megfelelően $v_1=-\frac{2}{9}$ és $v_2=\frac{4}{9}$. A keresett $a$ és $b$ értékek most már a $\begin{array}{c}{\displaystyle t^2-u_{1}t+v_1=\mathrm{0,}\text{illetve a}{t}^2-u_{2}t+v_2=0}\end{array}$ egyenletek megoldásai. Az első esetben $a=\frac{1}{3}-\frac{\sqrt[]{3}}{3}$ és $b=\frac{1}{3}+\frac{\sqrt[]{3}}{3}$, a második esetben viszont a két gyök egyenlő, $a=b=\frac{2}{3}$. A megoldást az $a\ne b$ feltétellel keressük, így a második lehetőség elesik. Ha $a=\frac{1}{3}-\frac{\sqrt[]{3}}{3}$, akkor $f\text{'}\left(a\right)=-\frac{8}{9}$ és $f\left(a\right)-a\cdot f\text{'}\left(a\right)=-\frac{4}{27}$, így az $\left(a;f\left(a\right)\right)$-beli érintő egyenlete $\begin{array}{c}{\displaystyle y=-\frac{8}{9}x-\frac{4}{27}\mathrm{.}}\end{array}$ Mivel lépéseink megfordíthatóak, ugyanez a $\left(b;f\left(b\right)\right)$-beli érintő egyenlete is.  Kármán Péter (Budapest, Móricz Zs. Gimn., 12. o.t.)   Megjegyzések. 1. Az $a=b=\frac{2}{3}$ az $y=3x^4-4x^3$ görbe ‐ egyik ‐ inflexiós pontjának az abszcisszája. Szigorúan véve itt is két egybeeső érintőről beszélhetünk, most azonban az érintési pontok is egybeesnek. 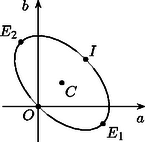2. A III. megoldásban kapott (3) feltételt ($\frac{f\text{'}\left(a\right)-f\text{'}\left(b\right)}{a-b}=0$) az $\left(a;b\right)$ koordináta-rendszerben ábrázolva egy ellipszist kapunk (3. ábra). Ez az ellipszis azokból a $P\left(a;b\right)$ pontokból áll, amelyekre az $\left(a;f\left(a\right)\right)$ és $\left(b;f\left(b\right)\right)$- pontokban az $y=3x^4-4x^3$ görbéhez párhuzamos érintők húzhatók. Az ellipszis tengelyei párhuzamosak a koordinátatengelyek szögfelezőivel, középpontja pedig a $C\left(\frac{1}{3};\frac{1}{3}\right)$ pont.   Az ellipszis kistengelyének végpontjai, $O$, és $I\left(\frac{2}{3};\frac{2}{3}\right)$ az $y=3x^4-4x^3$ görbe két inflexiós pontját adják. Első ránézésre meglepőbb, hogy a nagytengely végpontjai, $E_1\left(\frac{1}{3}+\frac{1}{\sqrt[]{3}};\frac{1}{3}-\frac{1}{\sqrt[]{3}}\right)$ és $E_2\left(\frac{1}{3}-\frac{1}{\sqrt[]{3}};\frac{1}{3}+\frac{1}{\sqrt[]{3}}\right)$ éppen a kettős érintő érintési pontjait szolgáltatják. Ez a kapcsolat világossá válik, ha átgondoljuk a negyedfokú görbe ,,szimmetriáját'' az $x=\frac{1}{3}$ pontra nézve. Ez az érték az érintők meredekségét számoló harmadfokú derivált grafikonja szimmetria-középpontjának az abszcisszája, és ha a negyedfokú polinomból kivonjuk a kettős érintő egyenletét, akkor a kapott negyedfokú görbe már valóban tengelyesen szimmetrikus lesz az $x=\frac{1}{3}$ egyenesre. (Ez indokolja ‐ többek között ‐ az I. megoldás helyettesítését.) Ez pedig azt jelenti, hogy a kettős érintő érintési pontjainak abszcisszái is szimmetrikusan helyezkednek el az $x=\frac{1}{3}$ pontra, a 3. ábrán a megfelelő pont rajta van az $a+b=\frac{2}{3}$ egyenletű egyenesen is, ami éppen az ellipszis nagytengelye. Könnyen ellenőrizhető, hogy ez a tulajdonság minden olyan negyedfokú görbére teljesül, amelynek létezik kettős érintője, pontosabban szólva az $\frac{f\text{'}\left(a\right)-f\text{'}\left(b\right)}{a-b}=0$ pontosan ebben az esetben lesz valós ellipszis egyenlete. Az így kapott ellipszisek hasonlók, excentricitásuk $\frac{\sqrt[]{3}}{3}$, állásuk olyan, ahogyan azt a 3. ábra mutatja, kistengelyük végpontjai a negyedfokú görbe inflexiós pontjait ‐ azaz a harmadfokú derivált szélsőértékeit ‐, nagytengelyük végpontjai pedig a kettős érintő érintési pontjait adják.       ${}^{*}$${}^1$