Kezdőlap


Feladat:	1999. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Gyenes Zoltán
Füzet:	1999/október, 392 - 393. oldal		PDF \| MathML
Témakör(ök):	Körérintők, Inverzió, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1999/szeptember: 1999. évi Nemzetközi Matematika Diákolimpia 22. feladata

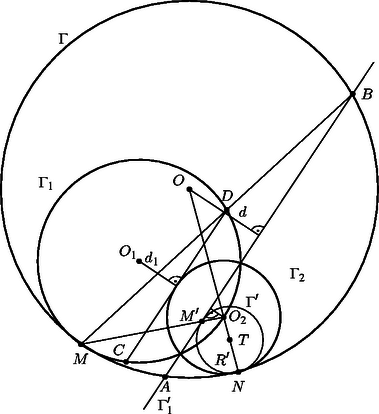
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először meghatározzuk az $O$ pont $A B$ -től mért $d$ távolságát (a távolságok végig előjelesek). Invertáljunk a $Γ_{2}$ körre. $Γ_{1}$ kör képe egyenes, mert átmegy az $O_{2}$ ponton; ezen az egyenesen vannak $Γ_{1}$ és $Γ_{2}$ közös pontjai, így $Γ_{1}$ képe az $A B$ egyenes. $Γ$ képe érinti $Γ_{1}$ , ill. $Γ_{2}$ képét, tehát az $A B$ egyenest és a $Γ_{2}$ kört; $A B$ -t $M$ képében, $M'$ -ben érinti ( $M'$ az $O_{2} M$ és $A B$ metszéspontja), $Γ_{2}$ -t $N$ -ben ( $N$ képe önmaga), tehát $Γ'$ középpontja, $T$ az $O N$ egyenes metszéspontja az $A B$ -re $M'$ -ben állított merőlegessel. A $Γ'$ kör átmérője, $2 R' = R_{2} + \frac{R_{2}^{2}}{2 R - R_{2}} = \frac{2 R R_{2}}{2 R - R_{2}}$ (ha $N$ átellenes pontja $Γ$ -n $U$ , $Γ'$ -n $U'$ , akkor az új átmérő hossza $N O_{2} + O_{2} U' = R_{2} + \frac{R_{2}^{2}}{O_{2} U}$ ).
Tehát $T$ távolsága $A B$ -től $\frac{R R_{2}}{2 R - R_{2}}$ .
$O_{2}$ távolsága az inverzió miatt $A B$ -től $\frac{R_{2}^{2}}{2 R_{1}}$ (ugyanis az $O_{2}$ -ből $A B$ -re bocsátott merőleges talppontja a $Γ_{1}$ kör $O_{2}$ -vel átellenes pontjának képe lesz.)

\begin{matrix} \begin{matrix} O_{2} T & = R_{2} - \frac{\frac{2 R R_{2}}{2 R - R_{2}}}{2} = \frac{R R_{2} - R_{2}^{2}}{2 R - R_{2}} = \frac{R_{2} (R - R_{2})}{2 R - R_{2}} \\ O O_{2} & = R - R_{2} \\ O T & = \frac{2 R (R - R_{2})}{2 R - R_{2}}, \end{matrix} \end{matrix}

tehát

\begin{matrix} \begin{matrix} λ & = \frac{O_{2} T}{O T} = \frac{R_{2}}{2 R} \\ 1 - λ & = \frac{O O_{2}}{O T} = \frac{2 R - R_{2}}{2 R} . \end{matrix} \end{matrix}

Ezekből látható, hogy ha

O

távolsága

A B

-től

d

, akkor

O_{2}

távolsága

A B

-től

\begin{matrix} λ \cdot d + (1 - λ) \cdot T M' = \frac{R_{2}^{2}}{2 R_{1}} . \end{matrix}

Tehát

\begin{matrix} d = \frac{1}{λ} \frac{R_{2}^{2}}{2 R_{1}} - \frac{1 - λ}{λ} \cdot \frac{R R_{2}}{2 R - R_{2}} = \frac{R R_{2}}{R_{1}} - R = \frac{R (R_{2} - R_{1})}{R_{1}} . \end{matrix}

Ebből kiszámolhatjuk

O_{1}

távolságát

C D

-től.

Γ_{1}

középpontosan hasonló

Γ

-hoz. A hasonlóság középpontja

M

, aránya

\frac{R_{1}}{R}

. A

Γ

-t

Γ_{1}

-be vivő hasonlóság

O

-t

O_{1}

-be,

A B

-t

C D

-be viszi, tehát

O_{1}

és

C D

távolsága

\begin{matrix} d_{1} = \frac{R_{1}}{R} \cdot d = R_{2} - R_{1}, \end{matrix}

ez éppen az igazolandó, mert így

O_{2}

távolsága

C D

-től

d_{1} + R_{1}

(

A B