Legyen $S$ egy ilyen ponthalmaz. Ekkor legyen az $S$-ben lévő pontok súlypontja $P$, és $e$ egy tetszőleges szimmetriatengely. Ha $e$-re tükrözzük az $S$ ponthalmazt, akkor ugyanehhez a ponthalmazhoz jutunk, tehát ha a súlypontját tükrözzük $e$-re, akkor önmagába megy át. Ez azt jelenti, hogy $P$ szükségképpen rajta van az $e$ szimmetriatengelyen, azaz a szimmetriatengelyek mind egy ponton mennek át.
Az $S$ halmaz tetszőleges két $A$, $B$ pontja egyenlő távolságra van $P$-től, mert $P$ a felező merőlegesükön van. Tehát $S$ pontjai mind ugyanakkora távolságra vannak $P$-től, azaz egy $P$ körüli körön vannak.
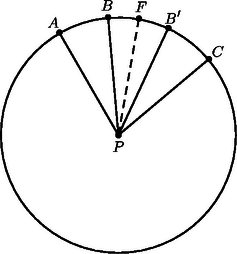
Tegyük fel, hogy $A$, $B$, $C$ három $S$-beli egymás melletti pont a körön ‐ azaz a $B$-t tartalmazó $AC$ íven a $B$-n kívül nincs más $S$-beli pont ‐, amelyekre $APB\sphericalangle <BPC\sphericalangle$. Ekkor legyen az $AC$ ív felezőpontja $F$. Feltevésünk miatt $B$ az $AF$ íven fog elhelyezkedni, tehát ha az $AC$ szakasz felező merőlegesére tükrözzük (ez éppen a $PF$ egyenes), a tükörkép az $FC$ íven lesz, nevezzük $B\text{'}$-nek. Az $AC$ szakasz felező merőlegese szimmetriatengelye $S$-nek, tehát $B\text{'}$ szükségképpen benne van az $S$ ponthalmazban. Ez viszont ellentmond azon feltevésünknek, hogy $A$, $B$, $C$ három egymás melletti pont a körön, mivel $B\text{'}$ az $FC$ íven van. Tehát $APB\sphericalangle =BPC\sphericalangle$ tetszőleges egymás melletti pontokra, azaz a szomszédos pontokat összekötő ívek hossza egyenlő, az $S$ pontjai egy szabályos sokszög csúcsai.
Megmutatjuk, hogy a szabályos $n$-szögek eleget is tesznek a feladat feltételeinek.
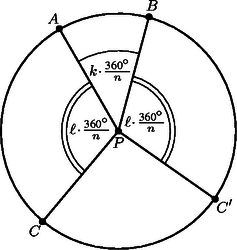
Két egymás melletti $Q$ és $R$ pontra $QPR\sphericalangle =\frac{2\pi }{n}$, és két tetszőleges csúcspont és a középpont által meghatározott szög ennek egész számszorosa.
Az $A$, $B$, $C$ pontok legyenek $S$ tetszőleges pontjai. Legyen