Feladat: 2001. évi Nemzetközi Matematika Diákolimpia 22. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Csikvári Péter 
Füzet: 2001/október, 392 - 393. oldal  PDF  |  MathML 
Témakör(ök): Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül, Háromszögek egybevágósága, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 2001/szeptember: 2001. évi Nemzetközi Matematika Diákolimpia 22. feladata

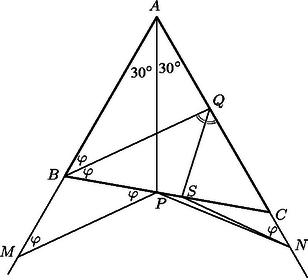
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az M pont az AB szakasz B-n túli meghosszabbításának az a pontja, amelyre BM=BP. Hasonlóan legyen N az AQ szakasz Q-n túli meghosszabbításának az a pontja, amelyre BQ=QN. A BQC szög felezője messe BC-t S-ben.
Legyen BPM∢=φ, ekkor BM=BP miatt BMP∢=φ és PBA∢=2φ. Tehát QBC∢=φ. A QBS és a QNS háromszögek egybevágóak, mert QB=QN, a QS oldaluk közös, továbbá SQB∢=NQS∢. Tehát QBS∢=QNS∢=φ. Így az AMP háromszög és az ANP háromszög is egybevágó, mert az

AM=AB+BM=AB+BP=AQ+BQ=AQ+QN=AN
oldalak egyenlőek, közös az AP oldaluk, és egyenlő az A-nál levő szögük. Ezért AMP∢=ANP∢=φ.
Tehát QNP∢=QNS∢=φ. Ekkor két eset lehetséges: P=S vagy P≠S, és így P, S, N egy egyenesen vannak.
Ha P=S, akkor a BQP és a QPN háromszögek, valamint az APM és APN háromszögek egybevágóságából kapjuk, hogy BP=PN=PM, azaz BP=PM=BM, azaz az ABC háromszög B-nél lévő szöge 180∘-60∘=120∘, ami nem lehetséges, mert így ABC∢+BAC∢=180∘.
Tehát P, S, N egy egyenesen vannak, azaz N=C. Így ABC∢=ANS∢=φ, azaz 180∘-BAC∢+ABC∢+ACB∢=60∘+2φ+φ. Innen φ=40∘ és 2φ=80∘. Tehát az egyetlen lehetséges megoldás, hogy ABC∢=80∘, ACB∢=40∘ és BAC∢=60∘.
Ez a megoldás jó is, mert a QBC∢=QCB∢ összefüggésből kapjuk, hogy BQ=QC. Továbbá az APM és APC háromszög egybevágó, mert két szögük, az A-nál, valamint az M és C-nél levő szögek megegyeznek, és van egy közös oldaluk: AP. Tehát AB+BP=AB+BM=AM=AC=AQ+QC=AQ+QB.
Tehát az egyetlen megoldás a 60∘, 80∘, 40∘-os háromszög.
 Csikvári Péter (Fazekas M. Főv. Gyak. Gimn., 11. o.t.)