Kezdőlap


Feladat:	2001. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Harangi Viktor
Füzet:	2001/október, 393 - 395. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Oszthatóság, Koszinusztétel alkalmazása, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 2001/szeptember: 2001. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kibontva $a c + b d$ szorzatalakját, majd rendezve az egyenlőséget a következőhöz jutunk:

\begin{matrix} a^{2} + b^{2} - a c = b^{2} + d^{2} + b d . \end{matrix}

(1)

(1)-ben pozitív egészek egyenlősége áll, és nyilván

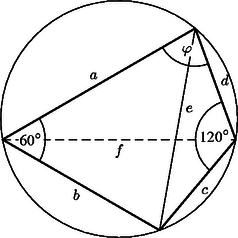
\begin{matrix} a^{2} + c^{2} - 2 a c cos 60^{\circ} = b^{2} + d^{2} - 2 b d cos 120^{\circ} . \end{matrix}

Ez pedig azt jelenti, hogy létezik olyan

e

hosszúságú szakasz, hogy az

a

c

e

oldalú háromszögben

e

-vel szemben

60^{\circ}

-os, a

b

d

e

oldalú háromszögben pedig

e

-vel szemben

120^{\circ}

-os szög van. Így az ábrán látható

a

c

b

d

oldalú,

e

átlójú négyszög húrnégyszög (két szemközti szögének az összege

180^{\circ}

). Használhatjuk tehát Ptolemaiosz tételét: ha

f

a másik átló hossza, akkor

\begin{matrix} a b + c d = e f . \end{matrix}

(2)

Most számoljuk ki

f

hosszát. Két koszinusztételt felírva:

\begin{matrix} a^{2} + d^{2} - 2 a d cos φ = f^{2} = b^{2} + c^{2} + 2 b c cos φ . \end{matrix}

Ebből

cos φ

-re a következő érték adódik:

cos φ = \frac{a^{2} + d^{2} - b^{2} - c^{2}}{2 (a d + b c)}

, amit visszahelyettesítve:

\begin{matrix} \begin{matrix} f^{2} & = a^{2} + d^{2} - 2 a d \cdot \frac{a^{2} + d^{2} - b^{2} - c^{2}}{2 (a d + b c)} = \frac{a^{2} b c + b c d^{2} + a b^{2} d + a c^{2} d}{a d + b c} = \\ = \frac{(a c + b d) (a b + c d)}{a d + b c} . \end{matrix} \end{matrix}

(3)

Ezt a kifejezést írjuk be (2) négyzetébe:

\begin{matrix} {(a b + c d)}^{2} = e^{2} f^{2} = e^{2} \frac{(a c + b d) (a b + c d)}{a d + b c} . \end{matrix}

Osztva

(a b + c d)

-vel:

\begin{matrix} a b + c d = \frac{(a c + b d) \cdot e^{2}}{a d + b c} . \end{matrix}

(4)

Legyen

P = a b + c d

Q = a c + b d

R = a d + b c

és

E = e^{2}

. Ekkor

P

Q

R

E

pozitív egészek, és (4) szerint

\begin{matrix} P R = E Q . \end{matrix}

(5)

Mivel

P - Q = (a - d) (b - c)

és

Q - R = (a - b) (c - d)

, azért

a > b > c > d

miatt

P > Q > R > 0

, és így (5)-ből

E > R > 0

.
Ha

P

prím, akkor

P ∣ E Q

miatt

P ∣ E

vagy

P ∣ Q

, és így

R = \frac{E}{P} \cdot Q = E \cdot \frac{Q}{P}

alapján

Q ∣ R

vagy

E ∣ R

. Mivel láttuk, hogy mind

Q

, mind pedig

E

nagyobb

R

-nél, egyik oszthatóság sem állhat fenn,

P

tehát valóban nem lehet prímszám.

Harangi Viktor (Fazekas M. Főv. Gyak. Gimn., 11. o.t.)