Kezdőlap


Feladat:	B.3396	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2001/április, 221 - 223. oldal		PDF \| MathML
Témakör(ök):	Diofantikus egyenletek, Feladat
Hivatkozás(ok):	Feladatok: 2000/október: B.3396

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vezessük be az egyelőre meghatározatlan $t$ paraméterrel az $u = x - t$ , $v = y - t$ , $v = z - t$ új ismeretleneket. Ezekkel az ismeretlenekkel az átrendezett $x y z - x y - y z - z x + 2 = 0$ egyenlet

\begin{matrix} u v w + (t - 1) (u v + v w + w u) + (t^{2} - 2 t) (u + v + w) + t^{3} - 3 t^{2} + 2 = 0 \end{matrix}

alakba írható. Mivel

t^{3} - 3 t^{2} + 2 = (t - 1) (t^{2} - 2 t - 2)

, látható, hogy

t = 1

választással a négy tag közül kettő lesz nulla, és az

\begin{matrix} u v w - u - v - w = 0 \end{matrix}

(1)

egyenlethez jutunk, ahol

u

v

és

w

nemnegatív egészek. Ezt fogjuk megoldani.
Ha

u

v

és

w

valamelyike nulla, akkor (1) szerint az összegük is az, és így az

u = v = w = 0

megoldást kapjuk. Föltehető ezért, hogy mindhárom érték legalább 1.
(1) bal oldala tovább alakítható:

\begin{matrix} (u v - 1) (w - 1) + (u - 1) (v - 1) - 2 = 0. \end{matrix}

(2)

Ha mindhárom érték legalább 2, akkor

u v \geq 4

, és így

(u v - 1) (w - 1) \geq 3

, amihez a nemnegatív

(u - 1) (v - 1)

-et adva nem kaphatunk

2

-t. Így

u

v

és

w

között van 2-nél kisebb, és mivel mindhárom érték legalább 1, egyikük ‐ például

w

‐ pontosan 1. Ekkor (2) így alakul:

\begin{matrix} (u - 1) (v - 1) = 2. \end{matrix}

(3)

A tényezők értéke nemnegatív, így a szorzat pontosan akkor 2, ha az egyik tényező 1, a másik pedig 2. Az

{u, v}

halmaz tehát a

{2, 3}

halmazzal egyenlő, így a szimmetrikus (1) nemnegatív megoldásai a

{0, 0, 0}

és az

{1, 2, 3}

számhármasok. Az eredeti egyenlet megoldásaira tehát vagy

{x, y, z} = {1, 1, 1}

, vagy pedig

{x, y, z} = {2, 3, 4}

.
Az egyenletnek így 7 megoldása van a pozitív egészek körében,

x_{1} = y_{1} = z_{1} = 1

, illetve a 2, 3, 4 számhármas hatféle permutációjaként adódó megoldások.

Megjegyzések. 1. A fentiekhez hasonló számolgatással könnyen ellenőrizhető, hogy az

x

y

z

számhármas pontosan akkor megoldása az eredeti egyenletnek, ha az

x_{1} = 2 - x

y_{1} = 2 - y

z_{1} = 2 - z

számhármas is megoldás. Mivel pedig az egyenletnek jól látható módon nincsen negatív egészekből álló megoldása (ekkor

x y

y z

z x

és

- x y z

mindegyike legalább 1), így az egyenletnek olyan megoldása sem lehet, ahol mindhárom érték nagyobb 2-nél.
Az egyenletet kielégítő pozitív számhármasok között tehát szerepelnie kell 3-nál kisebb értéknek is. Ha egy pozitív megoldásnak eleme a 2, például

x = 2

, akkor

x_{1} = 0

y_{1} = 2 - y

és

z_{1} = 2 - z

is megoldás, ami azt jelenti, hogy

y_{1} z_{1} = 2

. Innen vagy

{y_{1}, z_{1}} = {1, 2}

és így

{y, z} = {- 1, 0}

, ami nem pozitív megoldás, vagy pedig

{y_{1}, z_{1}} = {- 1, - 2}

és így

{y, z} = {3, 4}

; megkaptuk a

{2, 3, 4}

számhármast.
Azokat a pozitív megoldásokat nem találtuk még meg, amelyek elemei között nem szerepel a 2. Az ilyen megoldások legkisebb eleme az 1. Ha például

x = 1 \leq y

z

, akkor az egyenlet az

\begin{matrix} y + z = 2 \end{matrix}

alakot ölti, ez pedig a pozitív egész

y

és

z

értékekre csak úgy teljesülhet, ha

y = z = 1

.
2. Az egyenletből pl.

y

kifejezhető mint az

x

változó paraméteres (a paraméter

z

) racionális törtfüggvénye:

\begin{matrix} y = \frac{z x - 2}{(z - 1) x - z} . \end{matrix}

(4)

Ha az 1. megjegyzésben látottak szerint elintézzük azt az esetet, amikor valamelyik ismeretlen értéke 1, akkor a (3) függvényt abban az esetben kell vizsgálni, amikor

x

y

és

z \geq 2

, és mivel

x = y = z = 2

nem megoldás, az is föltehető, hogy

z > 2

.
A függvény grafikonján keressünk tehát rácspontokat az

x \geq 2

;

y \geq 2

feltételnek eleget tevő síknegyedben, amennyiben az egész értékű

z

paraméter értéke nagyobb 2-nél.
A függvény grafikonja szimmetrikus az

y = x

egyenesre, és az ábrán látható. A hiperbola aszimptotái az

x = z_{0}

és az

y = z_{0}

egyenesek, ahol

z_{0} = \frac{z}{z - 1}

. Mivel

z > 2

, azért

1 < z_{0} < 2

.
Ha

x = 2

, akkor

y = \frac{2 z - 2}{z - 2} > 2

, így a függvény grafikonján csak a

P Q

íven találhatunk rácspontot.
Az olvasóra bízzuk annak ellenőrzését, hogy ha

z > 4

, akkor a

P Q

íven sincsen rácspont, ha

z = 3

vagy 4, akkor pedig az első esetben csak a

(2, 4)

‐ és a szimmetrikus

(4, 2)

‐, a másodikban pedig csak a

(2, 3)

és a szimmetrikus

(3, 2)

rácspont esik a

P Q

ív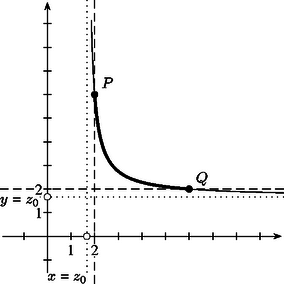re.