|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat jól látható módon két, egymástól majdnem független részből áll. Először megmutatjuk, hogy ha és pozitív egészek, akkor az liter űrtartalmú és a liter űrtartalmú edényekkel pontosan akkor mérhető ki 1 liter víz, ha és legnagyobb közös osztója 1. Ezek után a kérdés az, hogy az 1, 2, , 25 számok közül hányféleképpen választható ki tíz úgy, hogy közülük bármely kettő relatív prím legyen.
i) Ha egy adott helyzetben az edényben , a edényben pedig liter víz van, akkor a következő lépésben az egyes edényeket kiüríthetjük vagy színültig tölthetjük, ezen kívül bármelyik edény tartalmát elkezdhetjük átönteni a másikba, amíg az meg nem telik vagy az előbbi ki nem ürül. Bármely lépés után tehát legalább az egyik edény üres vagy tele van.
Egy liter víz kimérése ilyen körülmények között azt jelenti, hogy a fenti lépések véges sorozata után az egyik edényben 1 liter víz van. (A másik színültig van, vagy üres, ennek nincs jelentősége.)
Az feltétel nyilván szükséges, hiszen ha az és számok egy közös osztója, akkor a kezdetben üres edényekben lévő víz mennyisége nyilván osztható -vel, és ez a tulajdonság megmarad a fenti lépések bármelyikének a végrehajtása után is.
Másrészt, ha , akkor kimérhető 1 liter víz. Ha és , akkor az állítás semmitmondó, így föltehető, hogy például . A bizonyítás most már egy közismert aritmetikai állításon múlik:
Ha és , akkor az kongruenciának van megoldása,Ha ugyanis , akkor -nak két többszöröse, és akkor és csak akkor adja ugyanazt a maradékot -vel osztva, ha , vagyis miatt . Ezért, ha -nak vesszük a -vel osztva különböző maradékot adó 1, 2, , -szeres többszöröseit, akkor ezek is mind különböző maradékot adnak -vel osztva. Emiatt minden maradék pontosan egyszer fordul elő, lesz tehát köztük egy többszörös, amely 1 maradékot ad: . léteznek az és egészek, amelyekkel
Ezek szerint ha az edényt -szor megtöltjük, és az összesen liter vízből a edénnyel alkalommal összesen liter vizet eltávolítunk, akkor az edényben éppen 1 liter víz marad.
Az eljárás során időről időre ‐ összesen -szor ‐ liternél kevesebb víz marad az edényben, utoljára éppen 1 liter. Az utolsó alkalom kivételével ezt a maradványt ‐ az , , , mennyiségek -vel való osztásakor fellépő maradékot ‐ átöntjük a edénybe, és az edényt színültig töltve folytatjuk az eljárást.
Megjegyzések. 1. A fenti eljárás nyilván szimmetrikus, , esetben a kongruencia megoldásából kiindulva is kimérhető az 1 liter víz.
2. Mivel az adott feltételek esetén az kongruencia is megoldható tetszőleges esetén, azért tetszőleges egész esetén liter víz is kimérhető a két edénnyel.
3. A megoldásból kiderül, hogy tetszőleges pozitív egész , számokra pontosan akkor mérhető ki liter víz, ha és osztható az és legnagyobb közös osztójával, innen pedig teljes indukcióval egyszerűen adódik, hogy ugyanez kettőnél több edényre is igaz.
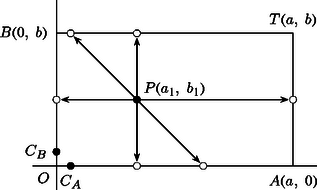
4. Érdekes geometriai szemléltetése adható a fenti bizonyításnak és magának a felhasznált tételnek is. Ha az edényekben , illetve liter víz van, akkor a rendszer állapota a ponttal, maga az eljárás pedig ennek a pontnak a pályájával ábrázolható (1. ábra). A folyamat során a pont az téglalap pontja, az ábra egy átmeneti állapotot mutat, amikor valamelyik edény tartalma változik. A vízszintes és a függőleges elmozdulások a megfelelő edények kiürítését, illetve feltöltését mutatják, az ,,átlós'' irányú elmozdulás pedig azt jelenti, hogy az egyik edény tartalmát átöntjük a másikba. A pont az origóból indul, útja során a megengedett irányok valamelyike mentén a téglalap határáig mozog, majd tovább folytatja útját.
A valóságosan elérhető állapotok így az téglalap kerületének egész koordinátájú pontjai közül kerülnek ki, az állítás pedig azt jelenti, hogy esetén van olyan pálya, amelyik áthalad a vagy a ponton. A 2. ábra az , esetben mutatja a megoldást.
Ha úgy tetszik, az ábrán látható ,,biliárd'' magát a kongruenciát ,,oldja'' meg. Az értéke a , a értéke pedig a falon történő ,,visszaverődések'' száma. Most és , és valóban: . A pont összesen ,,visszaverődés'' után érkezik a pontba, ami 13 átöntést jelent. A 3. ábra a szimmetrikus kongruencia megoldását mutatja a ,,biliárdasztalon''; ekkor és , most 8 visszaverődés után 9 átöntéssel érkezünk meg a pontba.
Mindkét ábrán ellenőrizhető, hogy ha tovább folytatjuk a megkezdett pályát, akkor az útvonal az téglalap kerületének valamennyi egész koordinátájú pontján áthaladva záródik az pontban, szemléltetve ezzel a 2. megjegyzésben mondottakat.
ii) Térjünk rá ezek után a feladat kérdésének megválaszolására. Vegyük észre először, hogy tíznél több szám nem választható ki az 1, 2, , 25 számok közül úgy, hogy közülük bármely kettő relatív prím legyen. A fenti számhalmazban ugyanis 9 prímszám található: 2 (4), 3 (2), 5 (2), 7 (1), 11 (1), 13 (1), 17 (1), 19 (1), 23 (1). A számok mögött zárójelben az a legnagyobb kitevő áll, amellyel a szóbanforgó prím a számhalmazban előfordul. Ha két szám relatív prím, akkor a prímtényezőik között nem lehet közös, így a tíz szám prímtényezőinek a halmazához a fenti 9-elemű halmaznak kell 10 darab, páronként közös elem nélküli részhalmazát kijelölnünk. Ez pedig csak úgy lehetséges, ha egyikük az üres halmaz ‐ az 1 tehát a kiválasztott számok között van ‐ a további 9 pedig a 9 darab egyelemű részhalmaz. A feltételeknek megfelelő 10-elemű halmazok tehát az | |
alakú halmazok, ahol , és . Ez összesen lehetőség, ennyiféleképpen választható ki 10 darab az első 25 pozitív egész közül úgy, hogy közülük bármely kettőnek 1 legyen a legnagyobb közös osztója.
|
 PDF |
PDF |  MathML
MathML