Feladat:	B.3387	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	2001/április, 213 - 214. oldal		PDF  |  MathML
Témakör(ök):	Vektorok, Pont körüli forgatás, Feladat
Hivatkozás(ok):	Feladatok: 2000/szeptember: B.3387

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha $\text{p}$  $\alpha$ és $2\alpha$ szögű elforgatottját $\text{p}\text{'}$-vel, illetve $\text{p}\text{'}\text{'}$-vel jelöljük, akkor a feltétel szerint $\text{p}+\text{p}\text{'}\text{'}=\text{p}\text{'}$, azaz $\begin{array}{c}{\displaystyle \text{p}-\text{p}\text{'}+\text{p}\text{'}\text{'}=\text{0}\mathrm{.}}\end{array}$ A három vektor, $\text{p}$, $-\text{p}\text{'}$ és $\text{p}\text{'}\text{'}$ abszolút értéke egyenlő és nem 0, így ha összegük $\text{0}$, akkor egymáshoz fűzve őket, három egyenlő szakaszból álló zárt töröttvonalat kapunk, ami azt jelenti, hogy a háromtagú zárt vektorlánc egy szabályos háromszöget alkot. 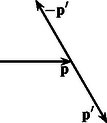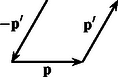Ez kétféleképpen lehetséges: ha pozitív körüljárás szerint a $\text{p}$ vektort a $-\text{p}\text{'}$ követi a láncban (1. ábra), illetve ha $\text{p}$, $\text{p}\text{'}\text{'}$ és $-\text{p}\text{'}$ a sorrend (2. ábra). 1. ábra   2. ábra Az első esetben a $\text{p}\text{'}$ vektor a $\text{p}$ vektor $-{60}^{\circ }$-os elforgatottja, a másodikban pedig, a fordított sorrend miatt, a $\text{p}\text{'}$ vektor a $\text{p}$ ${60}^{\circ }$-os elforgatottja. Az $\alpha$ szög tehát vagy $-{60}^{\circ }+n\cdot {360}^{\circ }$, vagy pedig ${60}^{\circ }+k\cdot {360}^{\circ }$, ahol $n$ és $k$ egész számok.   Megjegyzés. Látható, hogy az $\alpha$ szögre pontosan akkor teljesül a feladat feltétele, ha $\text{cos}\alpha =\frac{1}{2}$.   II. megoldás. Ha tetszőleges $\phi$ szög és $\text{p}$ vektor esetén $\phi \left(\text{p}\right)$ jelöli a $\text{p}$ vektor $\phi$ szögű elforgatottját, akkor a feltétel szerint $\begin{array}{c}{\displaystyle \text{p}+2\alpha \left(\text{p}\right)=\alpha \left(\text{p}\right)\mathrm{.}}\end{array}$ (1) Forgassuk most el az (1)-ben szereplő vektorokat $\alpha$ szöggel. Mivel vektorok összege tagonként forgatható, azért $\begin{array}{c}{\displaystyle \alpha \left(\text{p}+2\alpha \left(\text{p}\right)\right)=\alpha \left(\text{p}\right)+\alpha \left(2\alpha \left(\text{p}\right)\right)=\alpha \left(\alpha \left(\text{p}\right)\right)\mathrm{.}}\end{array}$ Elforgatott vektort továbbforgatva az eredő elforgatás szöge az elforgatások szögének összege, ezért $\alpha \left(2\alpha \left(\text{p}\right)\right)=3\alpha \left(\text{p}\right)$ és $\alpha \left(\alpha \left(\text{p}\right)\right)=2\alpha \left(\text{p}\right)$. Így $\begin{array}{c}{\displaystyle \alpha \left(\text{p}\right)+3\alpha \left(\text{p}\right)=2\alpha \left(\text{p}\right)\mathrm{.}}\end{array}$ (2) (1) és (2) összegét tekintve $\begin{array}{c}{\displaystyle \text{p}+\alpha \left(\text{p}\right)+2\alpha \left(\text{p}\right)+3\alpha \left(\text{p}\right)=\alpha \left(\text{p}\right)+2\alpha \left(\text{p}\right)\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle \text{p}+3\alpha \left(\text{p}\right)=\text{0}\mathrm{,}}\end{array}$ ha (1) teljesül, akkor a $\text{p}$ vektor $3\alpha$ szögű elforgatottja a $\text{p}$ vektor ellentettje, a $3\alpha$-val való forgatás ${180}^{\circ }$-kal forgatja el a $\text{p}$ vektort. Így $3\alpha ={180}^{\circ }+k\cdot {360}^{\circ }$, ahonnan ${\alpha }_1={60}^{\circ }$, ${\alpha }_2={180}^{\circ }$ és ${\alpha }_3={300}^{\circ }$. Mivel (1) és (2) összegét használtuk, a talált értékek nem feltétlenül megoldásai az eredeti feladatnak; valóban, ${\alpha }_2={180}^{\circ }$ láthatóan nem megoldás, ilyenkor $\text{p}+{360}^{\circ }\left(\text{p}\right)=2\text{p}$, ami nem egyenlő ${180}^{\circ }\left(\text{p}\right)=-\text{p}$-vel, ha $\text{p}\ne \text{0}$. A másik két érték, ${\alpha }_1={60}^{\circ }$ és ${\alpha }_2={300}^{\circ }$ láthatóan megoldások (3. ábra).   Megjegyzések. 1. A fenti megoldásban a $2\alpha \left(\text{p}\right)$ jelölés némi óvatosságot igényel: helyesebb volna $\left(2\alpha \right)\text{p}$-nek írni, hiszen az nem az $\alpha \left(\text{p}\right)$ vektor kétszerese, hanem a $2\alpha$ szöggel elforgatott $\text{p}$ vektor. 2. A feladat jelentése és a megoldás algebrai jellege a komplex számsíkon könnyen megmutatható. Ha az $\alpha$ szögű elforgatást az egységnyi abszolút értékű, $\alpha$ argumentumú $a$ számmal való szorzásként hajtjuk végre, akkor a feltétel szerint a $p\ne 0$ komplex számra $\begin{array}{c}{\displaystyle p+a^{2}p=ap\mathrm{,}}\end{array}$ ahonnan $p$-vel osztva az $\begin{array}{c}{\displaystyle a^2-a+1=0}\end{array}$ (3) másodfokú egyenletet kapjuk, amit $\left(a+1\right)$-gyel szorozva az $a^3+1=0$ egyenlet adódik. Ennek komplex gyökei, a komplex harmadik egységgyökök ellentettjei a (3) egyenlet megoldásai: $a_1=\text{cos}{60}^{\circ }+i\text{sin}{60}^{\circ }$ és $a_2=\text{cos}\left(-{60}^{\circ }\right)+i\text{sin}\left(-{60}^{\circ }\right)$. Innen is az ${\alpha }_1={60}^{\circ }$, ${\alpha }_2=-{60}^{\circ }$ adódik megoldásul, utóbbi természetesen ugyanaz, mint a ${300}^{\circ }$-os forgatás.   3. ábra   3. Ha tetszőleges forgásszögek is szóba jöhetnek ‐ a feladat szövegében nincs megszorítás a szögekre ‐, akkor természetesen végtelen sok megoldás adódik: ${\alpha }_k={60}^{\circ }+k\cdot {360}^{\circ }$, illetve ${\alpha }_n=-{60}^{\circ }+n\cdot {360}^{\circ }$, ahol $k$ és $n$ tetszőleges egész számok.