Feladat: B.3417 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Béky Bence 
Füzet: 2001/december, 531 - 532. oldal  PDF  |  MathML 
Témakör(ök): Mértani helyek, Kör egyenlete, Körsorok, Feladat
Hivatkozás(ok):Feladatok: 2000/december: B.3417

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az (x±2)2+y2-1=0 egyenletek két, egymást nem metsző és nem is érintő kör egyenletei. Ezért a sík bármely P(x0,y0) pontjának koordinátái legfeljebb az egyiket elégítik ki. Legyen

α0=(x0+2)2+y02-1ésβ0=-((x0-2)2+y02-1).(2)
Ekkor α és β egyszerre nem 0, és könnyű meggondolni, hogy a P pont akkor és csak akkor van rajta az (1) egyenlettel adott alakzaton, ha az (α,β) pár a (2) összefüggésekkel definiált (α0,β0) párból valamely számmal való szorzással keletkezik.
 
 

Azt is meg kell nézzük, hogy az így kapott egyenlet milyen α, β értékekre lesz kör egyenlete. Mivel x2 és y2 együtthatója megegyezik ‐ mindkettőé α+β ‐ azért ha ez nem 0, akkor az egyenlet vagy kör egyenlete, vagy egy ponté (a harmadik lehetőség az üres halmaz lenne ‐ pl. x2+y2+1=0 ‐, de most tudjuk, hogy alakzatunk tartalmazza P-t).
Ha α+β=0, akkor az (1) egyenletet rendezve kapjuk, hogy x=0. Vagyis az y tengely pontjai nincsenek rajta olyan körön, amelynek egyenlete (2) alakú.
Ha α+β≠0, akkor az (1) által meghatározott alakzat (kör vagy pont) szimmetrikus az x tengelyre, mert ha a Q(x1,y1) pont koordinátái kielégítik (1)-et, akkor a Q'(x1,-y1) pont koordinátái is. Ezért ha alakzatunk egyetlen pontból áll, akkor az a pont rajta van az x tengelyen. Ha α=0 ‐ és így β≠0 ‐, akkor (1) kör egyenlete. Ha a pontokat keressük, akkor tehát feltehetjük, hogy α≠0, s így azt is, hogy α=1 (egyenletünket beszorozhatjuk 1α-val). Rendezve az egyenletet:
(1+β)x2+(1+β)y2+(4β-4)x+3β+3=0.(3)
Ez pontosan akkor lesz egy, az x tengelyen lévő pont egyenlete, ha y=0 helyettesítés után az x-re kapott másodfokú egyenletnek kétszeres gyöke van, azaz ha diszkriminánsa 0. Ebből kapjuk, hogy
(4β-4)2-4(1+β)(3β+3)=0,
azaz β=7±43. Ezt visszaírva (3)-ba x=±3 adódik. Tehát a (±3,0) koordinátájú pontok sincsenek rajta olyan körön, amelynek egyenlete (1) alakú.
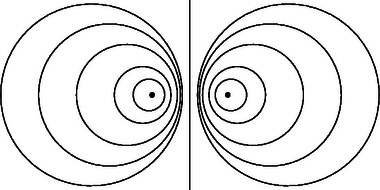
Összefoglalva tehát az x=0 egyenes pontjai, valamint a (±3,0) pontok felelnek meg a feladat feltételeinek.
 

Megjegyzés. A feladatban egy körsorhoz tartozó alakzatok egyenlete szerepel (a körsorokról lásd pl. Hajós György: Bevezetés a geometriába, 40.8). Mivel az α=1, β=0 és az α=0, β=1 párokhoz tartozó körök diszjunktak, azért a körsor elliptikus, annak semelyik két különböző eleme nem metszi egymást, a körsor elemei közt a körök mellett egy egyenes és két pont van. Az egyenes a körsor szimmetriatengelye (ábra).

 Béky Bence (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) dolgozata alapján