Feladat:	B.3418	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babos Attila ,  Balka Richárd ,  Béky Bence ,  Bóka Gergely ,  Herczegh Attila ,  Jelitai Kálmán ,  Kármán Péter ,  Kiss-Tóth Christián ,  Kocsis Albert Tihamér ,  Kőrizs András ,  Körtvélyessy Csaba ,  Maga Péter ,  Nagy 444 Zoltán ,  Nagy Ádám ,  Pogátsa Attila ,  Reiss Attila ,  Somogyi Dávid ,  Szekeres Balázs ,  Ta Vinh Thong ,  Tábor Áron ,  Takács Gergő ,  Tóth Ágnes ,  Tran Thanh Long ,  Zalán Péter
Füzet:	2001/november, 474 - 477. oldal		PDF  |  MathML
Témakör(ök):	Háromszög területe, Harmonikus közép, Geometriai egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 2000/december: B.3418

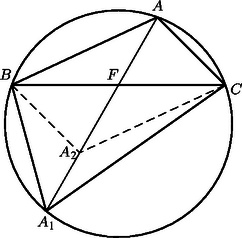
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az állítást először a nem hegyesszögű háromszögekre látjuk be. Legyen például $BAC\sphericalangle \ge {90}^{\circ }$. Ekkor $A$-nak a $BC$ oldal $F$ felezőpontjára való $A_2$ tükörképe a körülírt körre vagy annak belsejébe esik (1. ábra). Így az $A_{1}BC$ háromszög tartalmazza az $ABC$-vel egybevágó $A_{2}BC$ háromszöget, ezért a területe legalább $t_{ABC}$. 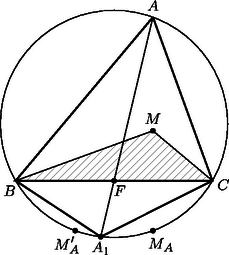Ha $ABC$ hegyesszögű, akkor az $M$ magasságpont a belsejébe esik, és ‐ mint ismeretes ‐ bármelyik oldalra vagy oldalfelező pontra való tükörképe a körülírt körön van. Jelölje az $M$ tükörképét a $BC$-re $M_A$, az $F$-re pedig $M_A\text{'}$ (2. ábra). Mivel az $AF$ egyenes elválasztja az $M_A$, $M_A\text{'}$ pontokat, azért $A_1$ az $M_A{M}_A\text{'}$ (rövidebb) körívre esik. Így $A_1$-nek a $BC$-től való távolsága legalább akkora, mint $M_A$-nak (illetve $M_A\text{'}$-nak) a távolsága $BC$-től. Ezért az $MBC$ háromszög területe legfeljebb akkora, mint az $A_{1}BC$ háromszögé, és pontosan akkor egyenlők, ha $M_A=M_A\text{'}$, azaz $AB=AC$. Hasonlóan kapjuk, hogy $T_{BMA}\le T_{B{C}_{1}A}$ és $T_{AMC}\le T_{A{B}_{1}C}$. A három egyenlőtlenséget összegezve a bizonyítandó állítást kapjuk, és az is látszik, hogy csak szabályos háromszögre van egyenlőség.  Nagy Ádám (Budapest, Szent István Gimn., 12. 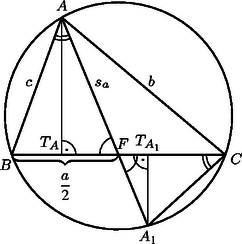o.t.)   II. megoldás. Jelöljük a háromszög oldalait $a$, $b$, $c$-vel, súlyvonalait pedig $s_a$, $s_b$, $s_c$-vel. Legyen a $BC$ oldal felezőpontja $F$, az $A$-ból, illetve $A_1$-ből a $BC$ egyenesre bocsájtott merőlegesek talppontjai pedig $T_A$, illetve $T_{A_1}$. Az $AFB$ és a $CF{A}_1$ háromszögek hasonlóak, mert $F$-nél lévő szögük csúcsszögek, továbbá $FC{A}_1\sphericalangle =BAF\sphericalangle$, mert azonos íven nyugvó kerületi szögek (3. ábra). Ezért megfelelő oldalaik aránya megegyezik, tehát $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{A_{1}F}{FC}=\frac{FB}{AF}\mathrm{,}}\\ \hfill {\displaystyle \text{ahonnan}}\\ \hfill {\displaystyle A_{1}F=\frac{FC\cdot FB}{AF}=\frac{\frac{a}{2}\cdot \frac{a}{2}}{s_a}=\frac{a^2}{4s_a}\mathrm{.}}\end{array}}}\end{array}$ Az $A{T}_{A}F$ és $A_1{T}_{A_1}F$ derékszögű háromszögek is hasonlóak, hiszen megfelelő szögeik egyenlőek. Így $\frac{A_1{T}_{A_1}}{A_{1}F}=\frac{A{T}_A}{AF}$, azaz $\begin{array}{c}{\displaystyle A_1{T}_{A_1}=\frac{A_{1}F\cdot A{T}_A}{AF}=\frac{a^2}{4s_a^2}\cdot A{T}_A\mathrm{.}}\end{array}$ (1) Az $A{T}_A$, illetve $A_1{T}_{A_1}$ szakaszok az $ABC$, illetve az $A_{1}BC$ háromszögek $BC$ oldalhoz tartozó magasságai, ezért az ismert területképlet szerint $\begin{array}{c}{\displaystyle A{T}_A=\frac{2t_{ABC}}{a}\mathrm{.}}\end{array}$ Ezt behelyettesítve (1)-be és ismét alkalmazva a területképletet, kapjuk, hogy $\begin{array}{c}{\displaystyle t_{A_{1}BC}=\frac{a\cdot A_1{T}_{A_1}}{2}=\frac{a}{2}\cdot \frac{a^2}{4s_a^2}\cdot \frac{2t_{ABC}}{a}=\frac{a^2\cdot t_{ABC}}{4s_a^2}\mathrm{.}}\end{array}$ Felhasználva az ismert $4s_a^2=2b^2+2c^2-a^2$ összefüggést, innen $\begin{array}{c}{\displaystyle t_{A_{1}BC}=\frac{a^2\cdot t_{ABC}}{2b^2+2c^2-a^2}\mathrm{.}}\end{array}$ Ugyanígy felírható $t_{B_{1}CA}$ és $t_{C_{1}AB}$ is. A bizonyítandó állítás tehát $\begin{array}{c}{\displaystyle \frac{a^2\cdot t_{ABC}}{2b^2+2c^2-a^2}+\frac{b^2\cdot t_{ABC}}{2c^2+2a^2-b^2}+\frac{c^2\cdot t_{ABC}}{2a^2+2b^2-c^2}\ge t_{ABC}\mathrm{.}}\end{array}$ Mivel $t_{ABC}>0$, azért azt kell megmutatnunk, hogy $\begin{array}{c}{\displaystyle S=\frac{a^2}{2b^2+2c^2-a^2}+\frac{b^2}{2c^2+2a^2-b^2}+\frac{c^2}{2a^2+2b^2-c^2}\ge 1.}\end{array}$ A számtani és a harmonikus közepek közti egyenlőtlenség szerint ha $x$, $y$, $z$ pozitív számok, akkor $\begin{array}{c}{\displaystyle x+y+z\ge \frac{9}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\mathrm{.}}\end{array}$ Az egyenlőtlenséget az $x=\frac{a^2}{2b^2+2c^2-a^2}$, $y=\frac{b^2}{2c^2+2a^2-b^2}$ és $z=\frac{c^2}{2a^2+2b^2-c^2}$ számokra felírva, ezután felhasználva, hogy egy pozitív számnak és a reciprokának az összege legalább 2, kapjuk, hogy $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle S}& {\displaystyle \ge \frac{9}{\frac{2b^2+2c^2-a^2}{a^2}+\frac{2c^2+2a^2-b^2}{b^2}+\frac{2a^2+2b^2-c^2}{c^2}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{9}{2\left(\frac{b^2}{a^2}+\frac{a^2}{b^2}\right)+2\left(\frac{c^2}{b^2}+\frac{b^2}{c^2}\right)+2\left(\frac{a^2}{c^2}+\frac{c^2}{a^2}\right)-3}\ge \frac{9}{2\cdot 2+2\cdot 2+2\cdot 2-3}=1.}\hfill \end{array}}}\end{array}$ Ezzel a feladat állítását beláttuk, s bizonyításunkból az is látszik, hogy egyenlőség akkor és csak akkor van, ha $a=b=c$, azaz ha $ABC$ szabályos háromszög.  Balka Richárd (Sárvár, Tinódi S. Gimn., 12. o.t.) dolgozata alapján