Feladat: A.251 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Csóka Endre ,  Hablicsek Márton ,  Kiss-Tóth Christián ,  Kunszenti-Kovács Dávid 
Füzet: 2001/október, 420 - 421. oldal  PDF  |  MathML 
Témakör(ök): Tetraéderek, Térgeometriai bizonyítások, Gömb és részei, Nehéz feladat
Hivatkozás(ok):Feladatok: 2000/december: A.251

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen Q egy, a feltételeknek megfelelő pont, és legyen a gömbre vonatkozó hatványa p. Tekintsük az A, B, AQ és BQ pontokat.
Az ABQ és BQAQQ háromszögek hasonlóságából

AQBQ=BQQ⋅ABAQ=BQ⋅BQQ⋅ABAQ⋅BQ=|p|⋅ABAQ⋅BQ.
Ugyanígy kapjuk, hogy
CQDQ=|p|⋅CDCQ⋅DQ.
Mivel az AQBQCQDQ tetraéder egyenlő oldalú, AQBQ=CQDQ. Behelyettesítve az előbbi eredményeket,
AQ⋅BQCQ⋅DQ=ABCD.

Teljesen hasonlóan
AQ⋅CQBQ⋅DQ=ACBDésAQ⋅DQBQ⋅CQ=ADBC.
E három egyenletből kiszámíthatjuk az AQ, BQ, CQ és DQ távolságok arányát:
AQ:BQ:CQ:DQ==AB⋅AC⋅AD:BA⋅BC⋅BD:CA⋅CB⋅CD:DA⋅DB⋅DC.

Mint ismeretes, azok a Q pontok, amelyekre az AQ:BQ arány egy megadott érték, egy gömbön vannak, amelynek középpontja az AB egyenesen van, és különbözik az A és B pontoktól. (Az ilyen gömböket Apollóniusz-gömböknek is nevezzük.) Ha az arány 1, akkor a gömb elfajul az AB szakasz felező merőleges síkjává. Hasonlóképpen azok a Q pontok, amelyekre az AQ:CQ, illetve AQ:DQ arány megfelelő, vagy az AC, illetve AD szakaszok felező merőleges síkján, vagy pedig egy olyan gömbön helyezkednek el, amelynek középpontja az AC, illetve AD egyenesen van, de nem eshet ezeknek a szakaszoknak a végpontjaiba. A továbbiakban megmutatjuk, hogy ennek a három Apollóniusz-gömbnek, illetve -síknak legfeljebb két közös pontja lehet. Jelöljük a három gömböt, illetve síkot Gb-vel, Gc-vel, illetve Gd-vel.
Ha Gb, Gc és Gd egyike sem fajul el és van három közös pontjuk, akkor a közös pontokon átmenő kör mindhárom gömbre illeszkedik. A közös kör t tengelye (a kör síkjára a középpontban állított merőleges egyenes) mindhárom gömb középpontját tartalmazza. A tengely tehát tartalmazza az AB, AC, AD egyenesek egy-egy, A-tól különböző pontját. Ebből viszont következik, hogy A és t síkja tartalmazza az AB, AC és AD egyeneseket, ezáltal a B, C és D pontokat is; ez viszont ellentmond annak, hogy az A, B, C és D pontok nincsenek egy síkban.
Ha az egyik Apollóniusz-gömb, mondjuk Gb síkká fajul, akkor csak úgy lehet kettőnél több közös pontja Gc-vel és Gd-vel, ha a Gb síkot a Gc és Gd gömbök ugyanabban a körben metszik. A közös metszet-kör t tengelye átmegy a Gc és Gd gömbök középpontján, tehát metszi az AC és AD egyeneseket, tehát az ACD síkban van. Ugyanakkor t merőleges a Gb síkra, vagyis párhuzamos az AB szakasszal. Ebből ismét az következik, hogy az A, B, C és D pontok egy síkban vannak, ami ellentmondás.
Ha két Apollóniusz-gömb, például Gb és Gc fajul síkká, akkor ezek különböző irányúak, mert merőlegesek a különböző irányú AB, illetve AC szakaszokra. A két sík tehát egy egyenesben metszi egymást. Ennek az egyenesnek a Gd gömbbel legfeljebb két közös pontja lehet.
Végül, ha mindhárom Apollóniusz-gömb síkká fajul, akkor egyetlen közös pontjuk van: az ABCD tetraéder körülírt gömbjének középpontja.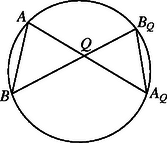