Feladat:	B.3441	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ambrus Gergely ,  Babos Attila ,  Backhausz Ágnes ,  Béky Bence ,  Birkner Tamás ,  Fehér Gergely ,  Hargitai Gábor ,  Kiss Demeter ,  Kiss-Tóth Christián ,  Lovrics Klára ,  Maga Péter ,  Nagy 444 Zoltán ,  Paulin Roland ,  Rácz Béla András ,  Somogyi Dávid ,  Szalay Zsófia ,  Tábor Áron ,  Tóth János
Füzet:	2001/október, 408 - 413. oldal		PDF  |  MathML
Témakör(ök):	Klasszikus valószínűség, Feladat
Hivatkozás(ok):	Feladatok: 2001/február: B.3441

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Vizsgáljuk először azt az esetet, amikor Pinokkiónak csak két akadállyal kell megbirkóznia, amelyeken a siker, illetve a kudarc valószínűsége $s_1$, $s_2$, illetve $b_1$, $b_2$. Ha Pinokkió pontosan $k$-szor bukik el a második akadályon ‐ itt $k$ tetszőleges természetes szám lehet ‐, akkor az első akadályon mindannyiszor újra át kell jutnia. Ekkor tehát a végső siker valószínűsége $p_k=s_1{\left(b_2{s}_1\right)}^k\cdot s_2$. Annak a valószínűsége tehát, hogy Pinokkió mindkét akadályon sikerrel jut át $\sum _{k=0}^{\infty }{p}_k$. Az összeg végtelen mértani sor, első tagja $s_1{s}_2$, hányadosa $b_2{s}_1$, ami most 0 és 1 közé esik. A sor tehát konvergens, összege $\begin{array}{c}{\displaystyle s=\frac{s_1{s}_2}{1-b_2{s}_1}\mathrm{.}}\end{array}$ (1) A nevező $1=b_1+s_1$ felhasználásával $b_2+s_1\left(1-b_2\right)=b_1+s_1{s}_2$, és így $\begin{array}{c}{\displaystyle s=\frac{s_1{s}_2}{b_1+s_1{s}_2}\mathrm{.}}\end{array}$ (2) Ha bevezetjük az $s_1*s_2=\frac{s_1{s}_2}{b_1+s_1{s}_2}$ jelölést, akkor látható, hogy a $*$ művelet nem kommutatív. $s_1*s_2$ és $s_2*s_1$ közül a számlálók egyenlősége miatt az a nagyobb, amelyiknek a nevezője kisebb. Így $s_1*s_2>s_2*s_1$ pontosan akkor teljesül, ha $b_1<b_2$, azaz $s_1>s_2$. Két akadály esetén tehát a könnyebb akadállyal kezdve lesz nagyobb esélye Pinokkiónak. A józan ész is ezt sugallja: érdemes a könnyebb feladatokkal kezdeni.   Megjegyzés. A talált eredmény és a tapasztalat általában is szemléletes választ sugall a feladat első kérdésére: az akadályok növekvő nehézségi sorrendjében számíthat Pinokkió a legnagyobb esélyre, és a fenti okoskodás egy teljes indukciós bizonyítás biztató kezdőlépéseként is felfogható. A gyors folytatáshoz arra volna szükség, hogy három ‐ vagy több ‐ akadály esetén tetszőleges sorrendben lehessen a szomszédos akadálypárok fenti ,,összevonásával'' az akadályok számát csökkenteni. 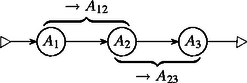Ez azonban nem teljesül, a művelet nem asszociatív: ha például $s_1=s_2=s_3=\frac{1}{2}$, akkor $s_1*s_2=s_2*s_3=\frac{1}{3}$, és így $\begin{array}{c}{\displaystyle \left(s_1*s_2\right)*s_3=\frac{1}{3}*\frac{1}{2}<\frac{1}{2}*\frac{1}{3}=s_1*\left(s_2*s_3\right)\mathrm{.}}\end{array}$ A továbblépéshez tehát az asszociativitás hiányában azt is meg kell vizsgálnunk, hogyan lehet három akadályt egyetleneggyel helyettesíteni: ebben az esetben is meg kell oldanunk a feladatot. Legyen most három akadály, $A_1$, $A_2$, $A_3$ ebben a sorrendben, és rajtuk a siker és kudarc valószínűsége $s_i$, illetve $b_i$ ($i=1$, 2, 3).     Ekkor az $\left(A_1\left(s_1\right)\mathrm{,}{A}_2\left(s_2\right)\right)$ akadálypárt a fentiek szerint az $A_{12}\left(s_1*s_2\right)$ akadállyal helyettesítve     helyes eredményt kapunk annak a valószínűségére, hogy Pinokkió eljut az $A_3$ akadály elé, ha azonban itt hibázik, akkor ,,felülről'' érkezik vissza az $A_{12}$ akadályhoz, és ebben az esetben a siker valószínűsége már nem ugyanaz az összevont és az eredeti változatban.   Megjegyzés. Könnyen meggondolható, hogy annak a valószínűsége, hogy Pinokkió ,,felülről'' érkezve sikerrel túljut az $A_1$, $A_2$ páron, $\sum _{k=0}^{\infty }{s}_2{\left(b_2{s}_1\right)}^k=\frac{1}{s_1}\cdot \left(s_1*s_2\right)$, így ezután az $s_1*s_2$ helyettesítés nem jogos. Az $\left(A_2\mathrm{,}{A}_3\right)$, illetve az őket helyettesítő $A_{23}\left(s_2*s_3\right)$     akadályhoz viszont Pinokkió már nem kerülhet ,,felülről'', hiszen ezt csak a célból visszafordulva tehetné meg. Ez azt jelenti, hogy az $A_1\left(s_1\right)$, $A_2\left(s_2\right)$, $A_3\left(s_3\right)$ akadályhármas az $A_1\left(s_1\right)$, $A_{23}\left(s_2*s_3\right)$ akadálypárral, ez utóbbi pedig, mint láttuk, az egyetlen $A_{123}\left(s_1*\left(s_2*s_3\right)\right)$ akadálypárral egyenértékű. A $*$ művelet tehát $s_1*\left(s_2*s_3\right)$ zárójelezéssel számítja ki helyesen a három akadályon való sikeres átjutás valószínűségét, innen pedig már adódik, hogy $n$ darab akadály esetén $\begin{array}{c}{\displaystyle s_1*\left(s_2*\left(\text{...}*\left(s_{n-1}*s_n\right)\text{...}\right)\right)}\end{array}$ (3) a megfelelő zárójelezés. A feladat megoldása ezek után kétféle módon fejezhető be. Az eddigiek és (2) alapján igazolhatjuk, hogy a (3) alatti mennyiség valóban akkor a legnagyobb, ha az akadályok növekvő nehézségi sorrendben követik egymást, majd (2) és (3) felhasználásával kiszámoljuk ezt az értéket, ha $n=9$, $s_1=\frac{9}{10}$, $s_2=\frac{8}{10}$, $\text{...}$, $s_9=\frac{1}{10}$. A másik lehetőségnek az látszik, hogy (2) alapján általános formulát keresünk a (3) kifejezésre, és ehhez keressük meg a maximális értéket adó elrendezést.   I. lehetőség. Mivel $n$ darab akadálynak $n!$ darab sorrendje létezik, ezek között van olyan, amikor a (3) értéke maximális. Megmutatjuk, hogy ha ebben az esetben az $s_i$ értékek nem csökkenő sorrendben követik egymást, azaz ha van olyan $1\le k<n$, hogy $s_k<s_{k+1}$, akkor a (3) kifejezés értéke növelhető, pontosabban $\begin{array}{c}{\displaystyle s_1*\left(s_2*\left(\text{...}{s}_k*\left(s_{k+1}*\text{...}*\left(s_{n-1}*s_n\right)\text{...}\right)\text{...}\right)\right)<s_1*\left(\text{...}*\left(s_{k+1}*\left(s_k*\text{...}*s_n\right)\right)\text{...}\right)\mathrm{,}}\end{array}$ a $k$-adik és a $\left(k+1\right)$-edik akadály cseréjével a siker valószínűsége nő. (1)-ből látható, hogy $s_1*s_2$ mindkét komponensében szigorúan monoton növő, és így elegendő igazolni, hogy $\begin{array}{c}{\displaystyle s_k*\left(s_{k+1}*\text{...}*\left(s_{n-1}*s_n\right)\text{...}\right)<s_{k+1}*\left(s_k*\text{...}*\left(s_{n-1}*s_n\right)\text{...}\right)\mathrm{,}}\end{array}$ azaz a $\left(k+1\right)$-edik utáni akadályok ‐ ha vannak ilyenek ‐ összevonása után $s_k<s_{k+1}$-ből $\begin{array}{c}{\displaystyle s_k*\left(s_{k+1}*s\right)<s_{k+1}*\left(s_k*s\right)}\end{array}$ (4) következik. (Ha $k+1=n$, akkor $s=1$ választással $s_{k+1}*1=s_{k+1}$, és $s_k*1=s_k$ miatt az állítás a két tagról látottak szerint teljesül.) (4) igazolásához egyszerűen fejtsük ki a két oldalt. (2) szerint $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle s_k*\left(s_{k+1}*s\right)=\frac{s_k\cdot \left(s_{k+1}*s\right)}{b_k+s_k\cdot \left(s_{k+1}*s\right)}=\frac{s_k{s}_{k+1}s}{b_k{b}_{k+1}+b_k{s}_{k+1}s+s_k{s}_{k+1}s}=\frac{s_k{s}_{k+1}s}{b_k{b}_{k+1}+s_{k+1}s}\mathrm{,}}\\ \hfill {\displaystyle \text{és ezután ugyanígy}}\\ \hfill {\displaystyle s_{k+1}*\left(s_k*s\right)=\frac{s_{k+1}{s}_{k}s}{b_{k+1}{b}_k+s_{k}s}\mathrm{.}}\end{array}}}\end{array}$ Mivel a számlálók egyenlők és a feltétel miatt a második tört nevezője kisebb, az állítás valóban igaz. Ezek után a maximális valószínűséget adó elrendezésben az akadályok lépésenként összevonhatók: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle s_8\text{'}}& {\displaystyle =s_8*s_9=\frac{2}{10}*\frac{1}{10}=\frac{1}{41};s_7\text{'}=s_7*s_8\text{'}=\frac{3}{10}*\frac{1}{41}=\frac{3}{290}\mathrm{,}}\hfill \\ \hfill {\displaystyle s_6\text{'}}& {\displaystyle =s_6*s_7\text{'}=\frac{4}{10}*\frac{3}{290}=\frac{1}{146};s_5\text{'}=s_5*s_6\text{'}=\frac{5}{10}*\frac{1}{146}=\frac{1}{147};}\hfill \\ \hfill {\displaystyle s_4\text{'}}& {\displaystyle =s_4*s_5\text{'}=\frac{6}{10}*\frac{1}{147}=\frac{1}{99};s_3\text{'}=s_3*s_4\text{'}=\frac{7}{10}*\frac{1}{99}=\frac{7}{304};}\hfill \\ \hfill {\displaystyle s_2\text{'}}& {\displaystyle =s_2*s_3\text{'}=\frac{8}{10}*\frac{7}{304}=\frac{7}{83}\mathrm{,}\text{végül}{s}_1\text{'}=s_1*s_2\text{'}=\frac{9}{10}*\frac{7}{83}=\frac{63}{146}\mathrm{.}}\hfill \end{array}}}\end{array}$ Pinokkió maximális esélye tehát $\frac{63}{146}\approx 0\mathrm{,}4315$.   II. lehetőség. Természetesebb alakot kapunk, ha a (2) összefüggés reciprokát tekintjük: $\begin{array}{c}{\displaystyle \frac{1}{s_1*s_2}=1+\frac{b_1}{s_1}\cdot \frac{1}{s_2}\mathrm{.}}\end{array}$ A jobb oldal második tagjában $\frac{1}{s_2}=\frac{s_2+b_2}{s_2}=1+\frac{b_2}{s_2}$, így ha $r_1=\frac{b_1}{a_1}$ és $r_2=\frac{b_2}{a_2}$, akkor $\begin{array}{c}{\displaystyle \frac{1}{s_1*s_2}=1+r_1\left(1+r_2\right)=1+r_1+r_1{r}_2\mathrm{,}}\end{array}$ és ez pontosan akkor kisebb, mint $\frac{1}{s_2+s_1}=1+r_2+r_1{r}_2$, ha $r_1<r_2$, azaz $s_1>s_2$. Innen egyszerű teljes indukcióval adódik, hogy $\begin{array}{c}{\displaystyle \frac{1}{s_1*\left(s_2*\text{...}*\left(s_{n-1}*s_n\right)\text{...}\right)}=1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_n\mathrm{,}}\end{array}$ (5) ahol $r_i=\frac{b_i}{s_i}$. A maximális valószínűséget adó elrendezést akkor kapjuk, amikor (5) jobb oldala minimális. Ha két szomszédos akadályt, a $k$-adikat és a $\left(k+1\right)$-ediket fölcseréljük, akkor a megfelelő összegekben azok a tagok, amelyek $r_k$-t és $r_{k+1}$-et egyszerre tartalmazzák vagy nem tartalmazzák, azonosak, így a két összeg nagyságviszonya az egy-egy megmaradó tag, $r_1{r}_2\text{...}{r}_{k-1}{r}_{k+1}$ és $r_1{r}_2\text{...}{r}_{k-1}{r}_k$ nagyságviszonyától, vagyis $r_{k+1}$ és $r_k$ nagyságviszonyától függ. Ha $r_{k+1}<r_k$, akkor a két akadály cseréjével a siker valószínűségének reciproka csökken, a kérdéses valószínűség tehát növekszik. A maximális valószínűséget adó elrendezésben tehát az $r_i$ értékek növekvően, az akadályok így a siker valószínűségének csökkenő sorrendjében vannak elrendezve. Pinokkió esetében ez az elrendezés az $r_i=\frac{i}{10-i}$ arányokat adja. Az $r_1\cdot r_2\cdot \text{...}\cdot r_i$ szorzat így $\frac{i!}{9\cdot 8\cdot \text{...}\cdot \left(9-i+1\right)}=\frac{1}{\left(\genfrac{}{}{0ex}{}{9}{i}\right)}$, a maximális valószínűség tehát: $\begin{array}{c}{\displaystyle \left({\left(\genfrac{}{}{0ex}{}{9}{0}\right)}^{-1}+{\left(\genfrac{}{}{0ex}{}{9}{1}\right)}^{-1}+\text{...}+{\left(\genfrac{}{}{0ex}{}{9}{9}\right)}^{-1}\right)=\frac{63}{146}\mathrm{.}}\end{array}$   II. megoldás. Ha az akadályok ebben a sorrendben $A_1$, $A_2$, $\text{...}$, $A_n$, és a $k$-adik akadályon $s_k$, illetve $1-s_k=b_k$ a siker és a kudarc valószínűsége, akkor jelölje $p_k$ annak a valószínűségét, hogy a $\left(k-1\right)$-edik akadályon túljutva Pinokkió igazi gyerek lesz. Ekkor a feladat kérdése éppen $p_1$-re vonatkozik. Érdemes két ,,mesterséges'' értéket is bevezetni, ezek $p_0=0$ és $p_{n+1}=1$. Előbbi azt a szomorú feltételt jelenti, hogy az első akadályon elbukva Pinokkió vállalkozása nem sikerül, utóbbi pedig azt, hogy ha az utolsó akadályon is sikerrel túljut, akkor a történet boldog véget ér. Ha Pinokkió sikerrel veszi a $k$-adik akadályt is ‐ ennek $s_k$ a valószínűsége ‐, akkor ezután $p_{k+1}$ eséllyel jut a célba; ha nem ‐ a kudarc valószínűsége a $k$-adik akadályon $b_k$ ‐, akkor újra kell próbálkoznia a $\left(k-1\right)$-edik akadályon, ahonnan $p_{k-1}$ a végső siker valószínűsége. Ez azt jelenti, hogy (6) (Vegyük észre, hogy $k=1$ és $k=n$ esetén a bevezetett $p_0=0$ és $p_{n+1}=1$ értékekkel (6) szintén teljesül.) Egy $n$-ismeretlenes egyenletrendszert kaptunk a bevezetett valószínűségekre, nekünk ezek egyike, $p_1$ értékét kell megtalálnunk. Algebrai lépések helyett nézzük meg, mit jelentenek geometriailag a (6) egyenletek.     A $p_k$ valószínűségek jelentéséből nyilvánvaló, hogy $0=p_0<p_1<\text{...}<p_n<1=p_{n+1}$, tehát a $p_k$ számok a $\left[0;1\right]$ intervallum egy felosztását adják. A $p_k=b_k\cdot p_{k-1}+s_k\cdot p_{k+1}$ egyenlet azt mondja, hogy a $p_k$ szám a $\left[p_{k-1};p_{k+1}\right]$ intervallumot     úgy osztja két részre, hogy $\frac{d_k}{d_{k-1}}=\frac{b_k}{s_k}$, azaz bevezetve az $r_k=\frac{b_k}{s_k}$ jelölést $\begin{array}{c}{\displaystyle p_{k+1}-p_k=d_k=r_k\cdot d_{k-1}\mathrm{.}}\end{array}$ (7) Innen ismételt helyettesítéssel kapjuk, hogy $d_k=r_1\cdot r_2\cdot \text{...}\cdot r_k\cdot d_0$, és így $d_0=p_1-p_0=p_1$, valamint $d_0+d_1+\text{...}+d_n=1$ miatt $\begin{array}{c}{\displaystyle 1=d_0+d_1+\text{...}+d_n=p_1\left(1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_n\right)\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle p_1=\frac{1}{1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_n}\mathrm{.}}\end{array}$ Lényegében az I. megoldás (5) formuláját kaptuk meg, innen a feladat megoldása az ott leírtak szerint fejezhető be.   Megjegyzések. 1. Az (7) egyenlőséget a (6) egyenletet átrendezéséből nyilván algebrai úton is megkaphatjuk. 2. Hasonlóan kapjuk, hogy a $p_k$ valószínűségek értéke $\begin{array}{c}{\displaystyle p_k=p_1\left(1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_{k-1}\right)=\frac{1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_{k-1}}{1+r_1+r_1{r}_2+\text{...}+r_1{r}_2\text{...}{r}_n}\mathrm{.}}\end{array}$ 3. Érdekes eredményhez jutunk, ha az egyes akadályokon a siker valószínűsége állandó. Ekkor $\frac{b_i}{s_i}=r$, és ilyenkor vizsgálhatjuk a siker valószínűségét, amennyiben az akadályok száma a végtelenhez tart. A bizonyítottak szerint $n$ akadály esetén $\begin{array}{c}{\displaystyle S=S\left(n\right)=\frac{1}{1+r+\text{...}+r^n}\mathrm{.}}\end{array}$ Ha $r\ge 1$ ‐ azaz $s\le \frac{1}{2}$ ‐, akkor a nevező nem korlátos, a siker valószínűsége nullához tart, ami szomorú, de nem meglepő. Ha viszont $r<1$, vagyis $s>\frac{1}{2}$, tehát Pinokkió többre képes, mint a vak véletlen, akkor a nevező konvergens, összege $\frac{1}{1-r}$, és így a siker valószínűsége sem csökken $1-r$ alá, akárhány akadállyal kell is szembenéznie Pinokkiónak.