Feladat:	B.3428	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balka Richárd
Füzet:	2001/szeptember, 355 - 357. oldal		PDF  |  MathML
Témakör(ök):	Körülírt kör, Geometriai egyenlőtlenségek, Beírt kör, Feladat
Hivatkozás(ok):	Feladatok: 2001/január: B.3428

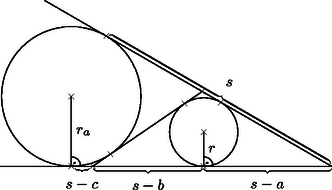
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Ha a háromszög oldalait $a$, $b$, $c$-vel, kerületét $2s$-sel, területét pedig $T$-vel jelöljük, akkor $\begin{array}{c}{\displaystyle T=r\cdot s=r_a\left(s-a\right)=r_b\left(s-b\right)=r_c\left(s-c\right)=\frac{abc}{4R}\mathrm{.}}\end{array}$ (1) (Ezeknek az összefüggéseknek a bizonyítása megtalálható pl. lapunk 2000/9. számának 532. oldalán.) Héron képletét, valamint (1)-et használva: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle r_a+r_b+r_c-r=\frac{T}{s-a}+\frac{T}{s-b}+\frac{T}{s-c}-\frac{T}{s}=}\\ \hfill {\displaystyle =\frac{T}{T^2}\left[(s\left(s-b\right)\left(s-c\right)+s\left(s-a\right)\left(s-c\right)+s\left(s-a\right)\left(s-b\right)-\left(s-a\right)\left(s-b\right)\left(s-c\right)\right]=}\\ \hfill {\displaystyle =\frac{1}{T}\left[\left(s-\left(s-a\right)\right)\left(s-b\right)\left(s-c\right)+s\left(s-a\right)\left(\left(s-c\right)+\left(s-b\right)\right)\right]=}\\ \hfill {\displaystyle =\frac{1}{4T}\left[a\left(a^2-{\left(b-c\right)}^2\right)+\left({\left(b+c\right)}^2-a^2\right)\cdot a\right]=\frac{1}{4T}a\left(4bc\right)=\frac{abc}{T}=4R\mathrm{.}}\end{array}}}\end{array}$ Vagyis a háromszög köré írható körének sugara egyszerűen kifejezhető a hozzáírt körök és a beírt kör sugarának segítségével. Eredeti feladatunk ezek után egyszerűen megoldható a számtani és a mértani közepek közötti egyenlőtlenség, illetve annak felhasználásával, hogy a körülírt kör sugara legalább kétszerese a beírt kör sugarának. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{r\cdot r_a\cdot r_b\cdot r_c}{R^4}\le \frac{r}{R}\cdot {\left(\frac{r_a+r_b+r_c}{3R}\right)}^3=\frac{r}{R}\cdot {\left(\frac{4R+r}{3R}\right)}^3=}\\ \hfill {\displaystyle =\frac{1}{27}\cdot \frac{r}{R}{\left(4+\frac{r}{R}\right)}^3\le \frac{1}{27}\cdot \frac{1}{2}\cdot {\left(4+\frac{1}{2}\right)}^3=\frac{27}{16}\mathrm{.}}\end{array}}}\end{array}$ Egyenlőség pontosan akkor teljesül, ha a háromszög szabályos.   II. megoldás. Ugyancsak az (1) összefüggéseket és Héron képletét felhasználva a bizonyítandó egyenlőtlenség $\begin{array}{c}{\displaystyle \frac{r\cdot r_a\cdot r_b\cdot r_c}{R^4}=\frac{T^4}{s\left(s-a\right)\left(s-b\right)\left(s-c\right)R^4}=\frac{T^2}{R^4}\le \frac{27}{16}\mathrm{,}}\end{array}$ azaz $\frac{T}{R^2}\le \frac{3\sqrt[]{3}}{4}$ alakra hozható. Tudjuk, hogy $T=\frac{a\cdot b\cdot \text{sin}\gamma }{2}$,  $R=\frac{a}{2\text{sin}\alpha }=\frac{b}{2\text{sin}\beta }$ ($\alpha$, $\beta$, $\gamma$ a háromszög szögei), ezért elég azt bizonyítani, hogy $\begin{array}{c}{\displaystyle \frac{T}{R^2}=2\text{sin}\alpha \text{sin}\beta \text{sin}\gamma \le \frac{3\sqrt[]{3}}{4}\mathrm{.}}\end{array}$ Mivel a $\text{sin}x$ függvény a $\left(\mathrm{0,}\pi \right)$ intervallumon pozitív és alulról konkáv, azért a számtani és mértani közép közötti, valamint a Jensen-egyenlőtlenséget felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle \text{sin}\alpha \cdot \text{sin}\beta \cdot \text{sin}\gamma \le {\left(\frac{\text{sin}\alpha +\text{sin}\beta +\text{sin}\gamma }{3}\right)}^3\le {\left(\text{sin}\frac{\alpha +\beta +\gamma }{3}\right)}^3={\left(\text{sin}{60}^{\circ }\right)}^3=\frac{3\sqrt[]{3}}{8}\mathrm{,}}\end{array}$ ami ekvivalens a bizonyítandó állítással. Egyenlőség csak szabályos háromszög esetén teljesül.  Balka Richárd (Sárvár, Tinódi S. Gimn., 12. o.t.) dolgozata alapján