Feladat:	B.3366	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dénes Attila ,  Kerékfy Péter ,  Sofró Csaba
Füzet:	2001/május, 286 - 287. oldal		PDF  |  MathML
Témakör(ök):	Síkgeometriai bizonyítások, Mértani helyek, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 2000/április: B.3366

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az alábbi ábrán a szöcske $A_1$ kiindulási pontja és további 7 pont tartózkodási helye látható: $B_1$, $A_2$, $B_2$, $A_3$, $B_3$, $A_4$ és $B_4$. Az ábra egy olyan esetet mutat, amikor a szöcske nem ugrik vissza oda, ahol az előbb volt. Azt szeretnénk kitalálni, hogy hová ugrik ezután a szöcske, mi lesz az $A_5$ pont (1. ábra). Mivel a bejelölt szakaszok mind egyenlő hoúak, így az $A_1{B}_1{A}_{2}O$ és az $A_2{B}_2{A}_{3}O$ négyszög is rombusz. Ebből következik, hogy az $A_1{B}_1$ és az $A_3{B}_2$ szakaszok is párhuzamosak és egyenlőek, tehát az $A_1{B}_1{B}_2{A}_3$ négyszög paralelogramma, az $A_1{A}_3$ szakasz párhuzamos a $B_1{B}_2$ szakasszal, azaz az adott egyenessel. Ha ugyanezt a gondolatmenetet úgy mondjuk el, hogy minden indexet 2-vel megnövelünk, akkor azt kapjuk, hogy az $A_3{A}_5$ szakasz is párhuzamos az adott egyenessel. Ez azt jelenti, hogy $A_1=A_5$. Mivel a szöcske minden helyről legfeljebb két másikra ugorhat tovább, így az $A_1$, $B_2$, $A_2$, $B_2$, $A_3$, $B_3$, $A_4$, $B_4$, $A_1$ ,,körút'' bármely pontjából csakis ezen pontok valamelyikébe ugorhat. Ezért e 8 ponttól különböző helyre még akkor sem juthat, ha lépésismétlések után más irányt próbálna választani.  Sofró Csaba (Budapest, Deák F. Gimn., 11. o.t.) és    Kerékfy Péter (Fazekas M. Főv. Gyak. Gimn., 10. o.t.) dolgozata alapján   II. megoldás. A feladatot komplex számok segítségével is megoldhatjuk. A kör középpontja lesz a 0, a valós tengelyt pedig az adott egyenesre merőlegesen vesszük föl (2. ábra). Mivel a szöcske a körről indul, így a páratlan sorszámú pontok a körön, a páros sorszámúak pedig az egyenesen vannak. Az ábráról leolvasható, hogy hová ugorhat tovább a szöcske: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle z_{2i+1}=z_{2i+1}-0=z_{2i}-z_{2i-1};}\\ \hfill {\displaystyle \text{és}}\\ \hfill {\displaystyle z_{2i+2}=z_{2i+1}+\overline{\left(z_{2i}-z_{2i+1}\right)}=z_{2i+1}-\overline{z_{2i+1}}+\overline{z_{2i}}\mathrm{,}}\end{array}}}\end{array}$ ahol $\overline{z}$ a $z$ szám komplex konjugáltját, azaz a valós tengelyre vonatkozó tükörképét jelöli. A fenti szabályok alapján: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle z_3}& {\displaystyle =z_2-z_1\mathrm{,}}\hfill \\ \hfill {\displaystyle z_4}& {\displaystyle =z_3-\overline{z_3}+\overline{z_2}=z_2-z_1-\overline{z_2}+\overline{z_1}+\overline{z_2}=z_2-z_1+\overline{z_1}\mathrm{,}}\hfill \\ \hfill {\displaystyle z_5}& {\displaystyle =z_4-z_3=z_2-z_1+\overline{z_1}-z_2+z_1=\overline{z_1}\mathrm{,}}\hfill \\ \hfill {\displaystyle z_6}& {\displaystyle =z_5-\overline{z_5}+\overline{z_4}=\overline{z_1}-z_1+\overline{z_2}-\overline{z_1}+z_1=\overline{z_2}\mathrm{,}}\hfill \\ \hfill {\displaystyle z_7}& {\displaystyle =z_6-z_5=\overline{z_2}-\overline{z_1}\mathrm{,}}\hfill \\ \hfill {\displaystyle z_8}& {\displaystyle =z_7-\overline{z_7}=\overline{z_2}-\overline{z_1}-z_2+z_1+z_2=\overline{z_2}-\overline{z_1}+z_1\mathrm{,}}\hfill \\ \hfill {\displaystyle z_9}& {\displaystyle =z_8-z_7=\overline{z_2}-\overline{z_1}+z_1-\overline{z_2}+\overline{z_1}=z_1\mathrm{,}}\hfill \\ \hfill {\displaystyle z_{10}}& {\displaystyle =z_8-\overline{z_8}=z_1-\overline{z_1}+z_2-z_1+\overline{z_1}+z_1=z_2\mathrm{.}}\hfill \end{array}}}\end{array}$ Tehát a szöcske a kilencedik ugrással az első pontba jut vissza, a tizedikkel pedig a másodikba. Ez így egy zárt ,,ciklus'', és a szöcskének mindig legfeljebb 2 választási lehetősége van, hogy merre ugorjon tovább, tehát más pontra nem ugorhat, valóban csak 8 pontba juthat el.  Dénes Attila (Békéscsaba, Rózsa F. Gimn., 12. o.t.)   Megjegyzések. 1. A II. megoldás nem igazán új az előzőhöz képest, de egy elegáns algebrai átfogalmazás. 2. A B. 3279. feladatban a szöcske két ‐ egymást ${36}^{\circ }$-os szöget bezáró ‐ egyenes között ugrált, most pedig egy egyenes és egy kör között. A tapasztalatok birtokában az olvasó bizonyára könnyen válaszolni tud az alábbi kérdésre: ha két olyan $r$ sugarú kör pontjai között ugrál a szöcske, amelyek nem mennek át egymás középpontján, akkor $r$ hosszúságú ugrásokkal legfeljebb hány pontba juthat el?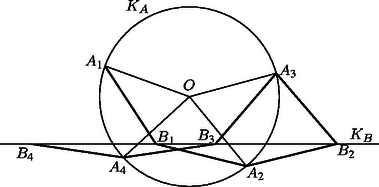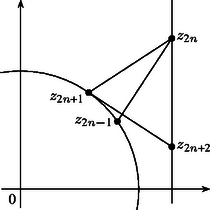