Kezdőlap


Feladat:	B.3411	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kiss-Tóth Christián
Füzet:	2001/április, 229 - 231. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometriával, Numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 2000/november: B.3411

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a sokszök köré írt kör sugara $r$ , a sokszög oldalszáma pedig $n$ . Ekkor a sokszög $n$ darab olyan egyenlő szárú háromszögre bontható, amelyek szárszöge $\frac{2 π}{n}$ , szárainak hossza pedig $r$ (1. ábra). Ezért a sokszög területe $T_{n} = n \cdot \frac{r^{2}}{2} sin \frac{2 π}{n}$ . Tudjuk, hogy a kör területe $T_{k} = r^{2} π$ . A sokszög akkor közelíti körülírt körének területét 1 ezreléknél kisebb hibával, ha teljesül a

\begin{matrix} \frac{T_{k} - T_{n}}{T_{k}} < \frac{1}{1000} \end{matrix}

egyenlőtlenség. A területképleteket beírva és rendezve kapjuk, hogy ez pontosan akkor teljesül, ha

\begin{matrix} n \cdot sin \frac{2 π}{n} > \frac{999}{500} π \approx 6, 276717. \end{matrix}

(1)

n = 81

, akkor (1) nem teljesülhet, mert

81 \cdot sin \frac{2 π}{81} < 6, 276887 < 6, 2769 < \frac{999}{500} \cdot π

. Ha

n = 82

, akkor viszont teljesül (1), mert

\frac{999}{500} \cdot π < 6, 277 < 82 \cdot sin \frac{360^{\circ}}{82}

.
Az a szemléletesen nyilvánvaló tény, hogy az oldalszám növelésével a sokszög mind jobban közelíti a körülírt kör területét, vagyis a hiba csökken, most azzal egyenértékű, hogy az

n \cdot sin \frac{2 π}{n}

n

-nek szigorúan monoton növő függvénye. A következőkben ezt igazoljuk.
Megmutatjuk, hogy

n \cdot sin \frac{2 π}{n}

n

-nek monoton növekvő függvénye, amiből következik, hogy (1) minden

n > 81

egész számra teljesül.
Legyen

x = \frac{2 π}{n}

. Elegendő azt belátnunk, hogy

\frac{sin x}{x}

monoton nő, ha

x

csökken (

0 < x < \frac{π}{2}

esetén). A 2. ábrán a

sin x

függvény grafikonjának egy darabja látható. Tudjuk, hogy

0 < x < \frac{π}{2}

esetén

x > sin x

, és a

sin x

grafikonja alulról nézve konvex. Ezért az

O B_{2}

egyenes az

A_{1} B_{1}

szakaszt egy belső

P

pontban metszi. Tehát ha

x_{1} < x_{2}

, akkor

\begin{matrix} \frac{sin x_{1}}{x_{1}} = \frac{A_{1} B_{1}}{O A_{1}} > \frac{A_{1} P}{O A_{1}} = \frac{A_{2} B_{2}}{O A_{2}} = \frac{sin x_{2}}{x_{2}}, \end{matrix}

amit bizonyítani akartunk.
Tehát a legalább 82 oldalú szabályos sokszögek 1 ezreléknél kisebb hibával közelítik körülírt körük területét.

Kiss-Tóth Christian (Fazekas M. Főv. Gyak. Gimn., 8. o.t.) dolgozata alapján

Megjegyzés. Nem egészen magától értetődő, hogy hogyan keressük meg az

n = 81

értéket. Kalkulátorral és némi türelemmel viszonylag gyorsan eljuthatunk ehhez az értékhez, de némi háttérismeret birtokában gyorsabban találjuk meg a keresett küszöböt.
Ismeretes, hogy ha

x

valós szám, akkor annak a szögnek a szinusza, amelynek

x

az ívmértéke, az alábbi végtelen sor öszege:

\begin{matrix} x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - ... + ... \end{matrix}

Erre persze most nincs igazán szükség, csak arra, hogy a váltakozó előjelű tagok hozzávételével felső, illetve alsó becslések (egyre finomodó) sorozatát nyerjük.
Minden pozitív

x

-re fennáll ezért a

\begin{matrix} sin x > x - \frac{x^{3}}{3!} \end{matrix}

(*)

egyenlőtlenség, ahonnan

x > 0

-val osztva

\frac{sin x}{x} > 1 - \frac{x^{2}}{6}

.
Ha most a vizsgált

n \cdot sin \frac{2 π}{n} > \frac{999}{500} π

egyenlőtlenséget a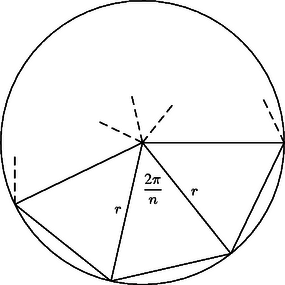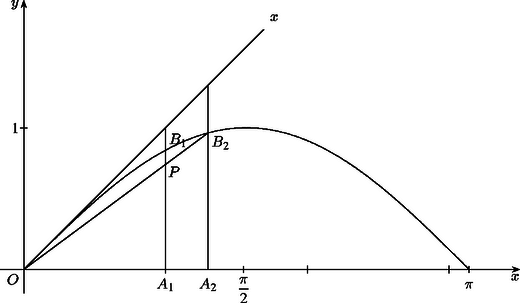

\begin{matrix} \frac{sin \frac{2 π}{n}}{\frac{2 π}{n}} > 0, 999 \end{matrix}

alakba írjuk, akkor ez bizonyosan teljesül, ha

\begin{matrix} \begin{matrix} 1 - \frac{{(\frac{2 π}{n})}^{2}}{6} > 0, 999, \\ ahonnan rendezés után \\ n > \frac{2 π}{\sqrt[]{0, 006}} \approx 81, 12. \end{matrix} \end{matrix}

(1) tehát biztosan teljesül, ha

n \geq 82

, az pedig, hogy

n = 81

-re nem teljesül, akár a kalkulátorral, akár pedig a

(*)

egyenlőtlenség hibájának ismeretében ‐ ez a hiba kisebb a következő tag,

\frac{x^{5}}{5!}

abszolút értékénél ‐ gyorsan eldönthető.