|
| Feladat: |
B.3401 |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Ambrus Gergely , Babos Attila , Balka Richárd , Balogh 541 János , Deli Lajos , Farkas Viktor , Gáti Beatrix , Hargitai Gábor , Horváth Illés , Jesch Dávid , Kiss-Tóth Christián , Kőrizs András , Maga Péter , Marton József , Nagy 469 Ambrus , Pach Péter Pál , Somogyi Dávid , Tóth 143 Anett , Tóth Ágnes , Tran Thanh Long , Zalán Péter |
| Füzet: |
2001/március,
159 - 164. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Számhalmazok, Egészrész, törtrész függvények, Szöveges feladatok, Konstruktív megoldási módszer, Feladat |
| Hivatkozás(ok): | Feladatok: 2000/október: B.3401 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Ha a raktárban csupa egyforma tömegű csomag van, amelyek közös tömege , akkor a teherautókra , illetve darab fér el, az elszállítható tömeg ilyenkor | |
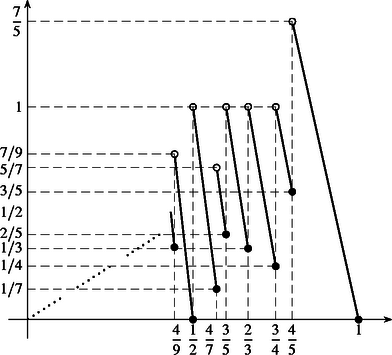
A ,,hiányt", a függvény grafikonját az ábrán láthatjuk.
Ez a hiányfüggvény a intervallumon értelmes, itt szakaszonként fogyó lineáris, azokban a pontokban szakad, ahol vagy értéke egész szám. A grafikont nyilván elegendő csak az -nél nagyobb -ekre vizsgálni, ennél kisebb súlyokkal ugyanis a két teherautó legfeljebb - tonnányi hiánnyal feltölthető.
Az is látható, hogy a függvénynek nincsen maximuma, a legnagyobb olyan hiány, ami már nem érhető el egyenlő súlyokkal, a .
Ha tehát tonnánál többet akarunk vállalni, akkor ez egyenlő súlyokkal megakadályozható. tonna terhet például már nem vállalhatunk, hiszen ha , akkor tonnás csomagokból a két teherautóra összesen darab fér, amelyek együttes tömege kisebb, mint .
Megmutatjuk, hogy legalább tonna terhet mindig el tudunk szállítani ‐ természetesen, ha van ennyi áru a raktárban. Osszuk ehhez a csomagokat két csoportra: legyenek a nehezek azok, amelyek tömege legalább tonna, a többiek pedig a könnyűek. Kezdjük el fölrakni a csomagokat az autókra, ha vannak nehezek, kezdjük ezekkel, majd ha ezek esetleg elfogytak vagy nincsenek, akkor a könnyűekkel folytatva ‐ ha vannak ilyenek ‐ egészen addig, amíg már egyik autóra sem tudunk több csomagot fölrakni.
Ez persze bekövetkezhetett azért, mert valamennyi csomagot fölraktuk már; ekkor nyilván teljesítettük, amit vállaltunk. Ha egy könnyű csomagnál akadtunk el, akkor mindkét teherautó kapacitását kevesebb, mint tonna hiánnyal használtuk ki, azaz a két teherautón összesen több, mint tonna teher van; most is teljesítettük, amit vállaltunk.
Az az eset maradt, ha egy nehéz csomag fölrakásakor akadunk el. Ekkor a nehéz csomagok együttes tömege több 6 tonnánál, hiszen az elakadáskor az egyik autót túlterheltük, a másikból pedig kevesebb, mint 1 tonna hiányzik. Pakoljunk le a teherautókról és tekintsük csak a nehéz csomagokat. Megmutatjuk, hogy már belőlük is fölrakható legalább tonna.
Ha van két olyan csomag, amelyek együttes tömege legalább tonna, akkor ezeket tegyük a kisebbik teherautóra. Ekkor itt még legalább egy tonna szabad hely marad, hiszen semelyik két csomag nem nehezebb 2 tonnánál. Ez azt jelenti, hogy a nagyobbik autót elakadásig rakva, az első csomagot, ami ott már nem fér, még éppen elhelyezhetjük a kisebbik teherautón. Így pedig összesen több, mint tonna súlyt raktunk föl.
Ha bármely két csomag együttes tömege tonna alatt marad, akkor könnyen látható, hogy ha , akkor bármely darab csomag együttes tömege is kisebb, mint tonna, tehát bármely öt csomag együttes tömege kisebb 4 tonnánál. Így bármely öt nehéz csomag elfér a nagyobbik autón, a kisebbiken pedig nyilván elfér három. A két autóra most összesen legalább nyolc darab nehéz csomag rakható, ezek együttes tömege pedig ismét legalább tonna.
Ezzel igazoltuk, hogy minden esetben elszállítható legalább tonna, ennél több azonban nem feltétlenül.
Megjegyzések. 1. A bizonyításból az is kiderül, hogy valójában minden esetben több, mint tonna terhet tudunk fölrakni az autókra, ezt azonban nem lehet ,,szerződésben vállalni''.
2. A fenti bizonyítás lényegében hasolóan működik, ha a két teherautó kapacitása , illetve tonna, ahol egész szám. A maximális vállalható teher ebben az esetben tonna.
3. A megoldás során felhasználtuk, hogy ha egy adott számhalmaz elemei közül bármely darab átlaga kisebb, mint , akkor minden esetén bármely darab átlaga is kisebb, mint . (A fenti bizonyításban és , a számok átlaga helyett pedig a számok összegéről beszéltünk.)
Egy elemű halmaz elemeiből összesen darab elemű halmaz készíthető. Eközben a minden egyes elemét ugyanannyiszor, -szer használtuk fel. A elemeiből készíthető tagú összegek összege tehát a elemei összegének a -szerese, ami a feltétel szerint kisebb, mint . A elemeinek az összege eszerint kisebb, mint és éppen ez a bizonyítandó állítás.
4. A megoldás során kiderült, hogy a maximum az egyenlő súlyokat feltételezve megkapható. Ez egyáltalán nem nyilvánvaló, az Interneten közölt megoldást követve erre adódik egy bizonyítás, ami azonban feltételezi, hogy a raktárkészlet elegendően nagy. Az alábbiakban Tardos Gábor nyomán bebizonyítjuk ezt az állítást.
II. megoldás. A következőt igazoljuk. Adottak az , , pozitív számok úgy, hogy és . Teljesül továbbá, hogy minden olyan számhalmazból A szokásos megszorítással ellentétben itt most megengedjük, hogy egy számhalmazban azonos elemek is szerepeljenek. Valójában helyesebb volna számok listájáról beszélni. , amelyik egyenlő, 1-nél nem nagyobb elemekből áll és amelyben az elemek összege legalább ld. a II. megoldáshoz fűzött 2. megjegyzést , kiválasztható két csoport úgy, hogy az egyik csoportban az elemek összege legfeljebb , a másikban pedig legfeljebb .
Azt állítjuk, hogy ekkor ugyanez a kiválasztás még akkor is megtehető, ha a halmaz elemeiről nem tesszük föl, hogy egyenlők.
Itt és nyilván a teherautók kapacitása. Megjegyezzük, hogy a bizonyítás során nem használjuk fel, hogy ezek a számok egészek. Vegyük észre viszont, hogy ha azok, akkor az megszorítás szükséges, hiszen ha a raktárban tonnánál bármilyen kicsivel nehezebb csomagok vannak, akkor ezekből összesen rakható föl, azaz tonnánál többet biztosan nem tudunk elszállítani.
A feladat állítása innen nyilvánvaló módon adódik. A függvény mutatja, hogy bárhogyan helyezünk el a raktárban egyenlő tömegű csomagokat, ha ezek együttes tömege legalább tonna, akkor a két teherautón elfér legalább tonna, .
Tekintsük tehát az halmazt. Először is feltehető, hogy az elemei közül bármelyiket elhagyva a megmaradó számok összege már alá csökken, a többi számot ugyanis ‐ ha vannak ilyenek ‐ egyszerűen elhagyhatjuk, a keresett számhalmazok elkészítése, azaz a teherautók feltöltése nélkülük is megvalósítható.
Jelölje a számok minimumát, ekkor tehát elemeinek az összege kisebb, mint . Legyen az elemeinek az átlaga, és tekintsünk egy olyan számhalmazt, amely csupa egyenlő, értékű számból áll. A feltétel szerint ekkor megoldható a feladat, léteznek tehát az és pozitív egészek úgy, hogy , és . Tekintsük most az eredeti számhalmazban az darab legnagyobb számot.
Ezek összege nyilván legalább . Ha szétoszthatók egy-egy , illetve elemű csoportra úgy, hogy az első csoport összege legfeljebb , a másodiké pedig legfeljebb , akkor készen is vagyunk. Ha ez nem megy, akkor közülük például egy elemű csoportban az elemek összege nagyobb, mint .
Tekintsük most az halmazban az darab legkisebb számot! Ezek átlaga nyilván legfeljebb , így összegük sem nagyobb, mint . Ha most ennek a minimális csoportnak az elemeit egyesével kicseréljük az előbbi ,,nehéz'' csoport elemeire ‐ a két csoportban persze lehet átfedés ‐, akkor lesz egy olyan állapot és egy ennek megfelelő elemű csoport, amelyben az elemek összege még kisebb, mint , de egy elemét egy másikra cserélve az összeg fölé nő. Mivel egy csere legfeljebb -mel növeli a halmaz elemeinek az összegét, azért elemeinek az összege, ami még nem nagyobb, mint , nagyobb, mint . Mivel elemeinek az összege kisebb, mint , azért a komplementerében az elemek összege kisebb, mint a halmaz és a komplementere tehát egy-egy megfelelő részhalmazt szolgáltat. Ezzel a bizonyítást befejeztük.
Megjegyzések. 1. A most bizonyítottak szerint elegendő az elszállítható maximális terhet azzal a többletfeltevéssel keresni, hogy a raktárban a csomagok tömege egyenlő. Ez az ábrán látható függvény felső határának vizsgálatát jelenti a intervallumon. Ezzel adott és egészekre véges sok érték maximumának a megtalálásává egyszerűsödik a feladat, nem látszik azonban egyszerűnek annak tisztázása, hogy miképpen függ ez az érték az és számoktól általában. Ha pedig és nem egészek ‐ márpedig a feladatban ezt semmi nem indokolja ‐, akkor a fenti bizonyításban felhasznált feltétel sem látszik szükségesnek. A probléma továbbá természetes módon terjeszthető ki kettőnél több teherautó esetére.
2. Érdekes változatát kapjuk a feladatnak, ha ‐ mint ahogyan ezt az Arany Dániel verseny döntőjében két versenyző is megtette A versenyfeladat szövege lehetővé tette ezt az értelmezést is. ‐ a feltételt némileg módosítva egy raktárost is közbeiktatunk, akinek az a dolga, hogy az általunk vállalt tömegű terhet ténylegesen összeállítsa. A feladatban így az eredeti változathoz képest a ,,legalább '' helyett pontosan összegű halmazt kell két, legfeljebb , illetve összegű részhalmazra osztani. Az eredeti , kapacitásokkal ilyenkor nagyobb érték, adódik, de most is igaz, hogy a maximális elszállítható terhet elegendő olyan számhalmazokon vizsgálni ‐ legalábbis ha egészek a kapacitások ‐, amelyekben az elemek egyenlők. Ennek bizonyítását az olvasóra bízzuk.
|
|
 PDF |
PDF |  MathML
MathML