Feladat:	B.3393	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Borgátai Diána
Füzet:	2001/március, 158 - 159. oldal		PDF  |  MathML
Témakör(ök):	Terület, felszín, Háromszög területe, Feladat
Hivatkozás(ok):	Feladatok: 2000/október: B.3393

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Kössük össze a $C$ és a $B\text{'}$ pontokat. Mivel $B\text{'}$ felezi $AA\text{'}$-t, azért $CB\text{'}$ felezi az $AA\text{'}C$ háromszög területét, és mivel $A\text{'}$ felezi $CC\text{'}$-t, azért $B\text{'}A\text{'}$ felezi a $CB\text{'}C\text{'}$ háromszög területét. Az $AA\text{'}C$ háromszög területe így kétszer akkor, mint az $A\text{'}B\text{'}C\text{'}$ háromszögé, és hasonlóan kapjuk ugyanezt az $AB\text{'}B$ és a $CC\text{'}B$ háromszögekre. Az $ABC$ háromszög területe tehát $2+2+2+1=7$-szer akkora, mint az $A\text{'}B\text{'}C\text{'}$ háromszög területe.   II. megoldás. Belátjuk, hogy a $CC\text{'}$ egyenes harmadolja az $AB$ szakaszt. $CC\text{'}$ a $P$-ben metszi az $AB$-t. $B\text{'}$-n keresztül húzzunk párhuzamost a $CC\text{'}$-vel. Ez az egyenes $AB$-t $Q$-ban metszi. A párhuzamos szelők tétele alapján, mivel $AB\text{'}=B\text{'}A\text{'}$, így $AQ=QP$. Ugyanígy, mivel $BC\text{'}=C\text{'}B\text{'}$, így $BP=PQ$. Vagyis $AQ=QP=PB$. A $B$, $C$ és $C\text{'}$ pontokon keresztül húzzunk párhuzamost $A\text{'}B\text{'}$-vel. Ekkor az előbb bizonyítottak alapján ezeknek a párhuzamosoknak a távolságai egyenlőek. Hasonlóan, a $B$, $B\text{'}$ és $A$ pontokon keresztül $A\text{'}C\text{'}$-vel húzott párhuzamosok távolságai is egyenlőek. Kaptunk 9 db egybevágó paralelogrammából álló nagy paralelogrammát, amely magában foglalja az $ABC$ és $A\text{'}B\text{'}C\text{'}$ háromszögeket. 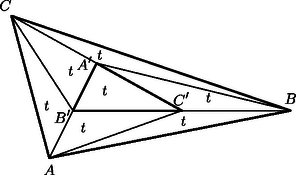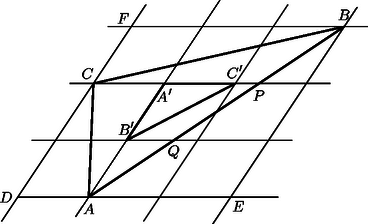A nagy paralelogramma területéből levonva az $EBA$, $BFC$ és $CDA$ háromszögek területét, az $ABC$ háromszög területét kapjuk (a kis paralelogramma területét tekintsük egységnyinek): $\begin{array}{c}{\displaystyle T_{ABC}=9-3-\frac{3}{2}-1=\frac{7}{2}\mathrm{,}{T}_{A\text{'}B\text{'}C\text{'}}=\frac{1}{2}\mathrm{.}}\end{array}$ Vagyis a területek aránya $1:7$.  Borgátai Diána (Székesfehérvár, Tóparti Gimn. és Művészeti Szki., 10. o.t.)