Kezdőlap


Feladat:	B.3385	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Béky Bence
Füzet:	2001/március, 154 - 155. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 2000/szeptember: B.3385

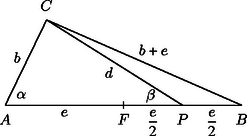
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A C = b$ , $C P = d$ , $\frac{1}{2} A B = e$ , ekkor $B C = b + e$ , legyen továbbá $P A C ∢ = α$ és $C P A ∢ = β$ (1. ábra). Be kell látnunk, hogy $α = 2 β$ .
Mivel $0^{\circ} < α, β < 180^{\circ}$ és a koszinuszfüggvény $0$ és $180^{\circ}$ között monoton csökkenő, így az eredetivel ekvivalens a $cos α = cos 2 β = 2 cos^{2} β - 1$ egyenlőség. Ezt fogjuk igazolni.
Írjuk fel a koszinusztételt az $A B C$ háromszögben az $α$ szögre, majd az $A C P$ háromszögben az $α$ , illetve $β$ szögekre:

\begin{matrix} \begin{matrix} {(b + e)}^{2} & = b^{2} + (2 e^{2}) - 4 b e \cdot cos α & (1) \\ d^{2} & = b^{2} + {(\frac{3}{2} e)}^{2} - 3 b e \cdot cos α & (2) \\ b^{2} & = d^{2} + {(\frac{3}{2} e)}^{2} - 3 d e \cdot cos α & (3) \end{matrix} \end{matrix}

Fejezzük ki (1)-ből

cos α

-t:

cos α = \frac{3 e - 2 b}{4 b}

; helyettesítsük be (2)-be:

\begin{matrix} d^{2} = b^{2} + \frac{9}{4} e^{2} - 3 e \frac{3 e - 2 b}{4} = b^{2} + \frac{3}{2} b e, \end{matrix}

ezt helyettesítsük (3)-ba, és fejezzük ki

cos β

-t:

\begin{matrix} cos β = \frac{b^{2} + \frac{3}{2} b e + \frac{9}{4} e^{2} - b^{2}}{3 d e} = \frac{2 b + 3 e}{4 d} . \end{matrix}

Lássuk be, hogy

cos α = 2 c o s^{2} β - 1

, azaz

\begin{matrix} \begin{matrix} \frac{3 e - 2 b}{4 b} & = 2 {(\frac{2 b + 3 e}{4 d})}^{2} - 1. \\ Mindkét oldalhoz 1-et hozzáadva: \\ \frac{3 e + 2 b}{4 b} & = 2 \frac{{(2 b + 3 e)}^{2}}{8 d^{2}} = \frac{{(2 b + 3 e)}^{2}}{4 (2 b^{2} + 3 b e)}, \end{matrix} \end{matrix}

ami valóban azonosság.

Béky Bence (Fazekas M. Főv. Gyak. Gimn., 11. o.t.)

Megjegyzések. 1. A beküldők többsége hasonló módon, általában bonyolultabb számolással oldotta meg a feladatot. Azonban ha valaki szinusztételt használt, akkor önmagában nem volt elég a

sin α = sin 2 β

egyenlőséget belátni, hiszen a

(0; π)

intervallumon a szinuszfüggvény nem kölcsönösen egyértelmű.
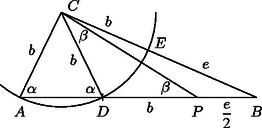
2. Lényegesen egyszerűbb a megoldás, ha abból kiindulva, hogy

B C = b + e

, rajzolunk

C

körül egy

b

sugarú kört. Ha ez a kör az

A B

-t

D

-ben,

C B

-t pedig

E

-ben metszi, akkor a 2. ábra jelöléseivel

C A = C D = C E = b

B E = e

.
Írjuk fel a

B

pontnak a körre vonatkozó hatványát kétféleképpen:

\begin{matrix} \begin{matrix} B E (B E + 2 C E) = B D \cdot B A, \\ azaz \\ e (e + 2 b) = B D \cdot 2 e, \end{matrix} \end{matrix}

ahonnan

B D = b + \frac{e}{2}

.

Mivel

P B = \frac{e}{2}

, így

D P = D B - P B = b

, tehát a

D P C

háromszög egyenlő szárú,

D C P ∢ = β

. E háromszög

D

csúcsánál

C D A ∢ = α

külső szög, így valóban

α = 2 β