Feladat:	B.3376	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Raikovich Tamás ,  Takács Gergő
Füzet:	2001/február, 98 - 100. oldal		PDF  |  MathML
Témakör(ök):	Háromszög területe, Esetvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 2000/május: B.3376

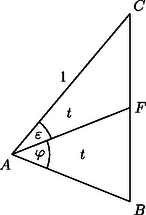
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $F$ a $BC$ oldal felezőpontja, ekkor $AF$ az $ABC$ háromszög súlyvonala. Legyen $CAB\sphericalangle =\epsilon +\phi$, ahol $CAF\sphericalangle =\epsilon$ és $FAB\sphericalangle =\phi$. Mivel a $CAF$ és az $FAB$ háromszögek területe egyenlő, igaz a következő: $\begin{array}{c}{\displaystyle t=\frac{AF\cdot AC\cdot \text{sin}\epsilon }{2}=\frac{AB\cdot AF\cdot \text{sin}\phi }{2}\mathrm{,}}\end{array}$ $AC=1$, tehát $AB=\frac{\text{sin}\epsilon }{\text{sin}\phi }$. Esetünkben a súlyvonal a $CAB$ szöget $1:2$ arányban osztja, így két eset lehetséges: a) $\phi =2\epsilon$ vagy  b) $\epsilon =2\phi$. Az a) esetben $AB=\frac{\text{sin}\epsilon }{\text{sin}2\epsilon }=\frac{\text{sin}\epsilon }{2\text{cos}\epsilon \cdot \text{sin}\epsilon }=\frac{1}{2\text{cos}\epsilon }$, és mivel $0^{\circ }<\epsilon +\phi <{180}^{\circ }$, így $0^{\circ }<\epsilon <{60}^{\circ }$, tehát $\frac{1}{2}<AB<1$. A b) esetben $AB=\frac{\text{sin}2\phi }{\text{sin}\phi }=\frac{2\text{cos}\phi \cdot \text{sin}\phi }{\text{sin}\phi }=2\text{cos}\phi$, és mivel most $0^{\circ }<\phi <{60}^{\circ }$, így $1<AB<2$. Az $AB$ oldal hossza tehát $\frac{1}{2}$ és 2 között lehet, de nem veheti fel az 1 értéket.  Raikovich Tamás (Győr, Czuczor G. Bencés Gimn., 10. o.t.)   II. megoldás. Megjegyzés. Ez a megoldás nem használ szögfüggvényeket, csak a háromszög-egyenlőtlenséget, ezért érdemes megismerni. 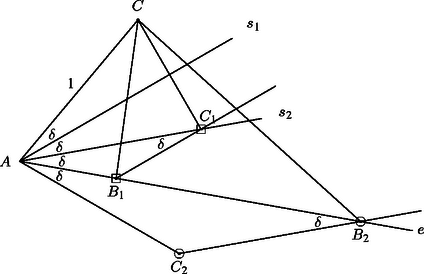Tekintsük az $ABC$ háromszög két csúcsát, $A$-t és $C$-t, valamint az $A$-nál levő $\alpha =3\delta$ szögét adottnak. Nevezzük $e$-nek az $AB$ egyenesét: a háromszög $B$ csúcspontja valahol ezen az egyenesen van. Mivel $\alpha <{180}^{\circ }$, így $\delta <{60}^{\circ }$. A 2. ábra jelölései szerint a háromszögnek vagy $s_1$, vagy $s_2$ a súlyvonala. Tükrözzük $C$-t $s_1$-re és $s_2$-re, legyenek a tükörképek $C_1$, illetve $C_2$. Ekkor $AC=A{C}_1=A{C}_2=1$, és $C_1$ nyilván rajta van $s_2$-n. Húzzunk $C_1$-en keresztül párhuzamost $s_1$-gyel és $C_2$-n keresztül párhuzamost $s_2$-vel; ezek metszéspontjai $e$-vel $B_1$, illetve $B_2$. Azt állítjuk, hogy ha az $ABC$ háromszög súlyvonala $s_1$, akkor $B\equiv B_1$, ha pedig $s_2$, akkor $B\equiv B_2$. Valóban, $s_1$ felezi a $C{B}_1$, $s_2$ pedig a $C{B}_2$ szakaszt. $B_1$ vagy $B_2$ mindig egyértelműen adódik mint $e$ és az $s_1$-gyel, illetve $s_2$-vel párhuzamos egyenesek egyetlen metszéspontja: $s_1$, $s_2$ és $e$ ugyanis nem párhuzamosak. Mivel $B_1{C}_1\Vert s_1$, így a $B_1{C}_{1}A\sphericalangle =\delta$, tehát az $A{B}_1{C}_1$ háromszög egyenlő szárú; hasonlóan, az $s_2$-re vonatkozó szimmetria miatt $C_{2}A{B}_2\sphericalangle =\delta$, és $B_2{C}_2\Vert s_2$ miatt $C_2{B}_{2}A\sphericalangle =\delta$, így az $A{C}_2{B}_2$ háromszög is egyenlő szárú. Az $A{B}_1{C}_1$ háromszögben $A{B}_1+B_1{C}_1=2A{B}_1>A{C}_1=1$ a háromszög-egyenlőtlenség miatt, tehát $A{B}_1>\frac{1}{2}$. Mivel $A{B}_1{C}_1\sphericalangle ={180}^{\circ }-2\delta >{60}^{\circ }$ ($\delta <{60}^{\circ }$) és a nagyobb szög nagyobb oldallal szemben van, így $A{B}_1<A{C}_1=1$. Azt kaptuk, hogy $\frac{1}{2}<A{B}_1<1$. Az $A{C}_2{B}_2$ háromszögben $A{C}_2+C_2{B}_2=2>A{B}_2$ a háromszög-egyenlőtlenség miatt, és $A{C}_2{B}_2\sphericalangle ={180}^{\circ }-2\delta >{60}^{\circ }$, így mivel nagyobb oldallal szemben kell hogy legyen a nagyobb szög, $A{B}_2>AC=1$, tehát $1<A{B}_2<2$. Tehát az $AB$ oldal hossza az egyik esetben $\frac{1}{2}$ és 1, a második esetben 1 és 2 közé esik, és itt bármilyen értéket felvehet, hiszen minden ilyen értékhez megszerkeszthető vagy az $A{B}_1{C}_1$, vagy az $A{C}_2{B}_2$ háromszög. (Vigyázat, $AB\ne 1$!)  Takács Gergő (Tatabánya, Árpád Gimn. és Pedagógiai Szki., 10. o.t.) dolgozata alapján