Egy háromszöget egyetlen vágással vagy két háromszögre, vagy egy háromszögre és egy négyszögre lehet darabolni. Ezért, mivel a részek között kell lennie háromszögnek is, ha két vágással három egybevágó részt kapunk, akkor mindhárom rész háromszög.
Kell, hogy legyen (legalább) egy olyan pont, amely mind a három háromszögnek határpontja. Ha ugyanis ilyen nem volna, akkor két egybevágó háromszöget a harmadik szétválasztana; ez egy-egy oldalon szomszédos volna a két szétválasztandó háromszöggel, ezen kívül további egy-egy oldalnak kellene biztosítani, hogy a két szélső háromszög határponton se érjen össze, így a középső háromszögben négy oldalnak kellene lennie.
A közös határpont helyzete háromféle lehet:
I. a határpont az eredeti háromszög belsejében van;
II. a határpont egy csúcsban van;
III. a határpont egy oldal belső pontja.
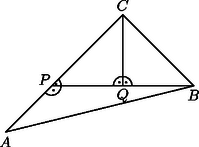
I. Ekkor biztos, hogy az egyik vágás végpontja a másiknak közbülső pontja, ugyanis különben nem kapnánk 3 háromszöget. Továbbá ahhoz, hogy háromszögeket kapjunk, mindkét vágás egyik végpontjának csúcsban kell lennie. Tehát a darabolás csak az 1. ábra szerinti lehet. Az ábra betűzését használva, mivel $PQC\sphericalangle +CQB\sphericalangle ={180}^{\circ }$, ezek nem lehetnek a két egybevágó háromszögnek két különböző szöge, így csak $PQC\sphericalangle =CQB\sphericalangle ={90}^{\circ }$ lehet. Hasonló okokból $APB\sphericalangle =CPB\sphericalangle ={90}^{\circ }$. Ekkor pedig a $CPQ$ háromszögben két derékszög volna, ami lehetetlen.
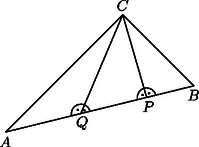
II. Legyen a határpont például a $C$ csúcsban. Most az előzőhöz hasonlóan az $AQC\sphericalangle$ és a $CQP\text{'}\sphericalangle$, mivel összegük ${180}^{\circ }$, nem lehetnek az egybevágó háromszögeknek különböző nagyságú szögei, így $AQC\sphericalangle =CQP\sphericalangle ={90}^{\circ }$, ugyanígy $BPC\sphericalangle =CPQ\sphericalangle ={90}^{\circ }$, tehát ismét két derékszög lenne a $CPQ$ háromszögben, így ez az eset sem lehetséges.
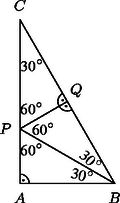
III. Legyen most a $P$ határpont az $AC$ oldalon. Ekkor a két vágás egyike a szemben fekvő csúcsba, a másik egy oldal belső pontjába megy, más esetben ugyanis nem kapnánk csupa háromszög darabot. Most az előzőekhez hasonló gondolatmenet miatt $PQC\sphericalangle =PQB\sphericalangle ={90}^{\circ }$. Nem lehet az $APB\sphericalangle ={90}^{\circ }$, mert akkor a $PAB$ háromszögben $PB$ befogó, a $PQB$ háromszögben pedig átfogó lenne, így nem volnának egybevágóak. A $P$-nél levő három szög összege ${180}^{\circ }$. Ha az egybevágó háromszögek derékszögtől különböző szögeit $\alpha$-val és $\beta$-val jelöljük, akkor vagy a$$) $2\alpha +\beta ={180}^{\circ }$, vagy b$$) $3\alpha ={180}^{\circ }$ lehet. Az a$$) eset nem fordulhat elő, hiszen $\alpha +\beta ={90}^{\circ }$, így a$$)-ból $\alpha ={90}^{\circ }$ következne. Marad tehát a b$$) eset, ekkor $\alpha ={60}^{\circ }$, $\beta ={30}^{\circ }$. Ez a darabolás a 3. ábra szerint meg is valósítható. (Az ismert $CB=2AB$ tulajdonság miatt a kis háromszögek egybevágóak.)
Így a feladat kérdésére a válasz: létezik ilyen darabolás, és csakis akkor, ha az eredeti háromszög (és egyúttal a keletkezett rész-háromszögek is) a derékszögű és ${60}^{\circ }$-os szögű háromszög, és a darabolás csak a III. esetben leírtak szerinti lehet.