| Feladat: | C.594 | Korcsoport: 14-15 | Nehézségi fok: könnyű |
| Megoldó(k): | Ásványi Katalin | ||
| Füzet: | 2001/február, 93 - 94. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Trapézok, Terület, felszín, Pitagorasz-tétel alkalmazásai, C gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 2000/szeptember: C.594 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A húrtrapéz olyan trapéz, amelynek oldalai a körnek húrjai, s mivel a húrnégyszög szemközti szögeinek összege , ebből következik, hogy a trapéz egyenlő szárú.
Ilyen trapéz akkor létezik, ha (2. ábra). A kétíves szögek egyenlők, mert egyenlő hosszúságú húrokhoz tartoznak, így , vagyis a négyszög valóban trapéz.
2. A szokásosnál több 0 pontos dolgozat oka az alábbi: Többen a következő hibás következtetéseket írták le: a) ,,Mivel a négyszög kerülete adott, és adott kerületű négyszögek közül a négyzetnek a területe a legnagyobb, ezért a négyszög négyzet.'' Ez a gondolat hibás, ugyanis nem csak a négyszög kerülete adott, hanem egyik oldala is, ezért (a esetet kivéve) a trapéz semmiképpen nem lehet négyzet. b) ,,A húrtrapézt a hosszabbik párhuzamos oldalára tükrözve hatszöget kapunk. Adott kerület esetén a szabályos hatszög területe a legnagyobb, ezért a húrtrapéz 3 oldala egyenlő, és -mal egyenlő.'' Ez a hiba hasonló az előzőhöz: a kapott húrtrapéznak a kerületén kívül egyik átlója is előre megszabott, így erre az általános szélsőérték-feladatra sem hivatkozhatunk. c) Voltak, akik a területet két egymástól nem független tag összegére bontották, és külön-külön keresték a maximumot, s ebből próbálták meghatározni a közös maximumot. 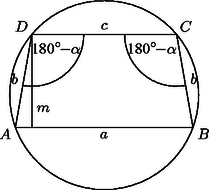 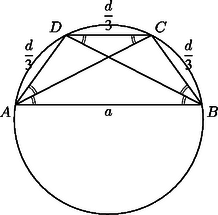 |